Mario Alemi's Blog

https://medium.com/media/8cbcbd899779f01c476c7bf3d6f3762b/href

Oggi commentiamo un articolo dal titolo “Electricity can be transmitted through the air”. Infatti, ci racconta l’economist, che la Nuova Zelanda –una compagnia neozelandese– sta rielaborando una vecchia idea e cercando di renderla commerciale. Questa vecchia idea viene definita il sogno di Tesla, ossia trasmettere l’energia elettrica attraverso l’aria.

Sì, trasmettere l’energia elettrica attraverso l’aria era uno dei sogni di Nikola Tesla. Tesla era un inventore senza… non era proprio uno scienziato, che ha iniziato a lavorare alla fine dell’ottocento, 1880 e passa, per una delle varie società di Edison a Parigi. Si è poi trasferito a New York dove sempre lavorato per Edison, ma non per molto tempo, e se n’è andato le voci dicono che sono andato perché Edison gli ha rubato un idea.

In realtà, lui stesso nella sua autobiografia –lui stesso Tesla– dice che se n’è andato perché la Machine Works Edison, la società per cui lavorava, non gli aveva dato un bonus che gli era stato promesso. In realtà il bonus di cui si parla è di circa l’equivalente di 10 milioni di dollari di oggi, ed era chiaramente uno scherzo del manager dell’azienda che lui ha preso seriamente, quindi se n’è voluto andare. Avevan detto “A chi fa questa cosa gli diamo un bonus di 10 milioni”. Lui l’ha fatta e voleva il bonus. Non gliel’hanno dato e se n’è andato.

Se n’è andato poi a lavorare per il nemico , diciamo il concorrente di Edison: George Westinghouse (c’è ancora adesso la società Westinghouse, fa centrali nucleari e resta un colosso) dove lavorano su un tipo di elettrificazione delle città diversa da Edison. Quindi ci sono due sistemi, a quel a quel tempo .
Uno è la corrente continua –quella che veniva utilizzata da Edison.

Come funziona la corrente continua? Semplicemente, diciamo che gli elettroni vengono inviati sempre nella stessa direzione. Quindi nella presa ci sarà un più e un meno. Nella spina ci sarà un polo caricato sempre positivamente quindi con pochi elettroni e un polo con molti elettroni. Oppure c’è la corrente alternata, in cui è un po’ come una pompa. Diciamo che nei fili elettrici si spingono gli elettroni e poi si ritiriamo indietro. Si spingono e si ritirano indietro. Quindi quando si mette la presa –quando facciamo andare una lampadina elettrica attaccandola alla presa– gli elettroni viaggiano prima in una direzione e poi nell’altra direzione. È alternata… Qual è la grossa differenza tra le due? Che la corrente alternata può ammazzare, la corrente continua è più difficile che uccida. Cioè se mettiamo le dita in una presa a corrente continua ci prendiamo una scossa e saltiamo in aria. La corrente alternata invece ci paralizza, e quindi restiamo lì attaccati finché non bruciamo come un fiammifero.

Quindi, anche giustamente, Edison e altri difendevano la corrente continua perché meno pericolosa. Westinghouse da parte sua difendeva la corrente alternata per il semplice fatto che era il futuro. Ricordiamo che a quei tempi gli Stati Uniti –alla fine dell’ottocento– erano molto ma molto indietro dal punto di vista scientifico rispetto all’Europa. Cioè… la scienza si faceva in Europa, non si faceva negli Stati Uniti. Quindi Westinghouse capisce che la corrente alternata, che viene utilizzata in quel periodo in europa, è il futuro perché molto più facile da generare. C’è un po’… quella che si chiama la “guerra delle correnti” negli Stati Uniti.

Gli Stati Uniti in quel periodo sono pieni di imbonitori, praticamente. Per cui, da parte sua Edison ammazza elefanti con la corrente alternata, e qualche decina di cani, sempre con la corrente alternata. Prima gli dà la corrente continua e fa vedere che non muoiono. Poi gli dà la corrente alternata e fa vedere che muoiono, e ammazzano un po’ di cani di questa in questa maniera. Alla fine comunque, come si sa, vincerà la corrente alternata.

Ma la cosa fondamentale è che Edison era un imprenditore-inventore, Tesla era più era un inventore… in quel periodo era l’inventore di punta della Westinghouse, perché non era lui stesso un grande imprenditore come Edison. Perché quindi è importante sognare la trasmissione dell’elettricità senza fili? Perché la gente moriva perché si attaccava al filo con la corrente alternata… quindi un certo punto Tesla progetta questo grande laboratorio.. Tesla poi se ne va dalla Westinghouse con qualche milione di dollari odierni perché gli venga il brevetto del motore a corrente alternata, e crea questa questo laboratorio in cui fa esperimenti per

trasmettere energia elettrica attraverso l’aria. Se Tesla ha venduto a Westinghouse il brevetto del motore a corrente alternata significa che l’ha inventato lui?

In realtà non l’ha inventato lui.

Come lui stesso riconosce ci è arrivato prima un ingegnere di Vercelli, un italiano, Galileo Ferraris, il quale però al contrario di Tesla non è ossessionato dai soldi, non è ossessionato dai brevetti, non pubblica sui giornali tipo il New York Herald Tribune o, come faceva Tesla, il Science and Inventions’ Magazine, il giornale delle intenzioni della scienza –un giornale illustrato– ma pubblica invece, Galileo Ferraris, su giornali scientifici.

La scienza tipicamente è aperta, quindi Galileo Ferraris inventa il motore a multifase, ne pubblica le specifiche sul suo giornale scientifico affinché chiunque possa utilizzarlo. Il brevetto di Tesla è un po’ diverso, poi siamo negli Stati Uniti, in realtà non si sa quello che succede in Europa come dice –come dicono entrambi Tesla e Galileo Ferraris– e quindi comunque Tesla riesce a brevettare il generatore o motore (dipende poi come come lo si fa andare).

Torniamo un momento all’articolo dell’economist: qual era il sogno di Tesla?

Il sogno di Tesla era quello di poter trasmettere energia esattamente come adesso si trasmettono i segnali radio. Quindi un’antenna fa broadcasting, trasmettere segnali radio ovunque e chiunque con la radiolina si può sentire il canale radio. Nel sogno di Tesla chiunque poteva mettere su un apparecchietto che avrebbe iniziato ad assorbire l’energia elettrica dall’aria e produrre energia elettrica… fornire energia elettrica. Proprio, lui dice potremmo andare in montagna con uno zainetto metterci là e poi attaccare la nostra presa a questo zainetto che prende energia dalla montagna.

Come dice la società che di cui parla l’economist, la EMROD, Tesla sognava una trasmissione omni-direzionale. Quello che è stato fatto oggi ovviamente è una trasmissione mono-direzionale. Quindi c’è una specie di tubo virtuale in cui viaggia l’energia, le microonde, che poi vengono rivelate dall’altra parte… esattamente le microonde del forno. Vengono rivelate da un’altra parte e invece di scaldare l’acqua producono energia elettrica nell’antenna che sta lontano. Perché delle microonde? Perché tutti conosciamo il laser, ma prima del laser fu inventato il maser (microwave amplification by…) quindi è abbastanza.. è relativamente facile costruire una specie di laser.

Immaginiamoci come le microonde del forno, che però viaggiano come un laser, quindi un tubo. Qual è il problema? Che ovviamente se ci passa un uccellino dentro viene cotto… poi l’uccellino ci passa in fretta, però non è carino. Quindi l’idea molto simpatica della EMROD è quella di mettere tipo dei laser come da discoteca, quindi a bassa potenza, tutto attorno a questo cilindro virtuale, per cui se un uccellino entra nel raggio di azione –entra in questo cilindro in cui viaggiano le microonde– automaticamente viene rilevato, la trasmissione viene interrotta, l’uccellino passa e la trasmissione viene ripresa. Sia la EMROD con questo cilindro, sia le altre due società che vengono citate nell’articolo –che sono la Powerlight Technologies, che lo conoscevo, e la Mitsubishi, che è una delle più grandi società al mondo che tutti conosciamo queste le ultime due invece è un tiggiano proprio il maser.

Raccontiamo un po’ di più sulla trasmissione di impulsi elettrici.

Tesla, quando ha costruito questa antenna per la trasmissione di energia ha anche costruito delle antenne per la ricezione dei segnali elettrici. E la cosa divertente che incominciò a ricevere dei segnali da Marte –secondo lui– perché riceveva del codice morse. Il povero Tesla non sapeva che mentre appunto negli Stati Uniti in quel periodo giocavano a cowboy e indiani, e la scienza era abbastanza indietro, dall’altra sponda dell’oceano –dove c’era dove si faceva Scienza con la S maiuscola– l’italiano Guglielmo Marconi già aveva messo su una società enorme per la trasmissione dei segnali via aria alle navi.

Un altro piccolo inciso nell’inciso. Marconi la società “Marconi” l’ha fatta purtroppo a Londra, perché come sempre in Italia non è che c’è la fuga dei cervelli: c’è l’espulsione dei cervelli. Marconi era di famiglia nobile, quindi aveva buoni contatti. Tanto buoni contatti che riuscì a inviare la propria scoperta al ministro dell’industria, mi sembra, il quale annotò sulla lettera di Marconi “Da mandare al manicomio.” Al ché Marconi pensò bene di andar via da questo paese, andare a Londra, dove immediatamente le Poste Inglesi (le poste!) capirono l’importanza della scoperta e lo aiutarono, gli diedero i fondi per creare un impero. Ricordiamo che l’italia
–lo dico ogni volta– l’Italia ha prodotto diciamo uno dei cinque più grandi geni al mondo, che è Galileo Galilei, e ha rischiato di bruciarlo vivo
Galileo Galilei.

Il libro più importante di Galileo Galilei, che è “Dialogo sulle due scienze” è stato pubblicato in Olanda, da quella che poi è diventata la più grande casa editrice di giornale scientifici, perché in Italia Galileo non poteva pubblicare. Fermi è che un altro di quelli che può stare sulle dita di una mano dei più grandi scienziati mai esistiti, Enrico Fermi se n’è dovuto andare via perché sua moglie era ebrea. In realtà l’Europa… non ci rendiamo conto dell’emorragia che c’è stata all’inizio del secolo scorso dall’Europa verso gli Stati Uniti, e di come veramente la scienza fosse una cosa europea, all’inizio del novecento, non c’erano gli Stati Uniti. Cioè l’unico lo scienziato degno di nota negli Stati Uniti in quell’epoca è Millikan, che aveva scoperto la carica… misurato la carica –era uno sperimentale– la carica dell’elettrone. Ma tutta la scienza veniva fatta in Europa.

(dal video “L’Economist della Settimana”)

https://youtu.be/WMUFADyEX2o

L’articolo di questa settimana è il necrologio di Paul Crutzen,
morto il 28 gennaio scorso.

Una figura importantissima, colui che ha introdotto il concetto di “Antropocene” o “epoca dell’uomo”.

Non è l’unica cosa che ha fatto, e infatti ha vinto il premo Nobel nel 1995 per aver fatto una scoperta importantissima –ossia che i clorofluorocarburi, che prima si trovavano in ogni frigorifero e bomboletta spray, erano i responsabili del buco dell’ozono.

Poi è stato lui a introdurre il concetto di “inverno nucleare”. Sia il buco nell’ozono sia l’inverno nucleare sono concetti che abbiamo sentito tutti. Ma l’Economist insiste soprattutto su un terzo merito: la creazione dell’Antropocene…

L’Economist parla di Crutzen soprattutto in merito alla all’introduzione del termine Antropocene. Che cos’è l’antropocene? I geologi dividono la vita della terra in tante età esattamente, come facciamo noi esseri umani per noi: abbiamo l’infanzia, l’adolescenza… Ogni età è divisa in sotto-età e così via. L’Antropocene è un’età della terra che è stata introdotta –ma non ancora definitivamente accettata– nel 2000 proprio da Paul Crutzen, ed è, come dice il termine, l’età in cui la terra sente l’influenza dell’anthropos, dell’essere umano.

Tipo il giurassico, che è il periodo centrale in cui sono esistiti di dinosauri.

L’antropocene non è stato ancora accettato definitivamente, siamo nell’Olocene. L’Olocene è una epoca –le epoche durano 10–100 mila anni è iniziata 11.000 anni. Cosa è successo 11 mila anni fa ? C’è stata la fine dell’ultima grande glaciazione…

La cosa interessante però è che 10 mila anni fa è success,o dal nostro punto di vista, qualcosa di fondamentale: cioè l’essere umano ha iniziato a utilizzare l’agricoltura.

Nel senso che l’ha inventata?

No, secondo molti antropologi non c’è stata una vera e propria invenzione dell’agricoltura 10.000 anni fa.

Fino a 10.000 anni fa eravamo ancora cacciatori raccoglitori. Ogni tribù andava in giro, prendeva i frutti, un po’ cacciava gli animali… l’essere umano poteva prendere abbastanza dalla natura senza bisogno di forzarla a produrre qualcosa. Cioè la natura da sola produceva abbastanza per sostenere tutta l’umanità.

10.000 anni fa siamo arrivate essere così tanti che la natura da sola non poteva più fornire abbastanza cibo, roba da mangiare, e quindi siamo stati obbligati ad aumentare la produttività della natura. Come l’abbiamo fatto? L’abbiamo fatto con l’introduzione dell’agricoltura e della pastorizia… super-semplificando, però… Dieci mila anni fa c’è stata un’epoca nuova importante dal nostro punto di vista, ma anche dal punto di vista del pianeta terra, che improvvisamente si è trovata una specie che ha cominciato a trasformarla. Perché l’agricoltura è una trasformazione attiva dell’uomo dell’ambiente…
Questo processo ha permesso all’umanità di crescere continuamente abbiamo cominciato a coltivare sempre di più, ad allevare sempre gli animali e siamo arrivati ad essere su tutto il pianeta Terra più di mezzo miliardo.

A questo punto però la terra, ancora, non ce la faceva più: comunque non poteva sostenere più di mezzo miliardo di persone. E quindi abbiamo iniziato a cercare delle fonti alternative, e nel 1700 in Inghilterra abbiamo iniziato a utilizzare… l’essere umano ha iniziato ad utilizzare il carbone. Questo è l’inizio veramente di una nuova era, cioè il momento in cui l’essere umano non si accontenta più, diciamo, di piegare ai propri bisogni la produttività del pianeta Terra, ma addirittura va sotto terra e prende ciò che la natura aveva scartato.

Cioè tutte quelle piante che erano state sotterrate e da micro-organismi trasformate in petrolio e carbone, vengono prese dall’essere umano, tirate su, e utilizzate per produrre energia per sostentarsi. Quindi nel 1700 e poi nel 1850 con l’inizio dell’estrazione del petrolio negli Stati Uniti c’è veramente l’inizio di una “nuova era”. Per noi che iniziamo utilizzare il petrolio, ma soprattutto per la terra che si vede ritornare in superficie tutto quel materiale che aveva un po’ “nascosto” sotto il tappeto. Non è che noi stiamo facendo qualcosa di innaturale –il petrolio e lì e lo stiamo bruciando– però abbiamo iniziato a tirarlo su, a bruciarlo e a lasciare un’impronta ecologica enorme sul pianeta.

Quanta energia consumiamo oggi grazie al petrolio?

Noi, come come primati, consumiamo circa 2000 calorie al giorno (le calorie sono un’unità di misura dell’energia). Se andiamo a prendere l’energia che noi utilizziamo in forma di elettricità, motori a scoppio, centrali eoliche e compagnia ogni persona non consuma più 2000 calorie ma –almeno in Europa– ne consuma 100.000. Per quanto riguarda il pianeta Terra, il peso energetico di un essere umano equivale al peso energetico di 50 scimpanzé.
Non avevo la minima idea che consumassimo un quantitativo così immenso di energia.

Se approssimiamo il numero di esseri umani a 10 miliardi, e moltiplichiamo per 50, abbiamo che la popolazione umana pesa sul pianeta Terra come peserebbero non 10 miliardi ma 500 miliardi di scimpanzé. L’Antropocene è qualcosa di veramente ultra-reale. Se uno scienziato marziano arrivasse sulla terra e si trovasse 500 miliardi di scimpanzé, che vuol dire che ricoprirebbero tutto il pianeta Terra come un formicaio, direbbe: “Ok, questo è un pianeta in cui questa specie di scimpanzé veramente ha monopolizzato l’ecosistema”. Noi non ce ne rendiamo conto perché in realtà siamo degli ingordi energetici. Per cui non siamo 500 miliardi siamo tra virgolette solo 10 miliardi, però il nostro peso sulla terra è veramente incredibile, è veramente notevole.

E quando finirà il petrolio –perché il petrolio finirà?

Quando finirà il petrolio: o si trova una alternativa, oppure vuol dire che il povero pianeta obiettivamente non è in grado di sostenere una simile sanguisuga energivora, una specie che utilizza così tanta energia. Per cui vuol dire che o troviamo una fonte di energia alternativa –qualcosa abbiamo trovato: eolico, solare ma siamo lontani dal poter produrre tutta l’energia che ci serve con queste fonti alternative– oppure banalmente la popolazione umana, come spesso accade –nelle specie che hanno colonizzato la terra, le specie di vita che hanno colonizzato la terra– dovrà diminuire,
dovrà restringersi.

Il pianeta terra sicuramente non potrà sostenere il 10 miliardi di esseri umani.

Quindi ci ridimensioneremo a qualche milione, tanti quanti eravamo 10.000 anni fa, banalmente.

Politica monetaria e investimenti pubblici: dalla pastorizia alle startup.

(dal video “L’Economist della Settimana”)

https://medium.com/media/45f5eedc665a46db694ceacd1380776b/href

L’articolo di questa settimana è “The real revolution on Wall Street”.
Le transazioni finanziarie sembra che costino sempre meno. Un bene o un male? Secondo l’Economist –anche se può creare qualche problema inizialmente– a lungo termine sarà un bene.

Questo, a ben vedere, è un trend che probabilmente ha avuto origine con l’invenzione della moneta.

Per capire la funzione della moneta, proviamo a immaginarci una storia, successa qualche migliaio di anni fa.

Le prime civilizzazioni di allevatori vedevano la pecora, la pecunia-pecora, come il bene principe che poteva essere scambiato. Capitalismo deriva, del resto, da caput, capo di bestiame.

Se io avevo bisogno di un paio di scarpe andavo dal calzolaio, gli davo una pecora e lui mi dava un taglio di scarpe.

E se io mi trovavo con nessuna pecora, ma un bellissimo asinello?

Mettiamo che, normalmente, l’asino viene scambiato per due pecore. Ma siccome in quel momento io ho necessità delle scarpe, non essendoci la moneta devo ricorrere –siccome c’è solo il baratto– a un intermediario.

Ossia, devo barattare il mio asino con delle pecore: così avrò delle pecore, e poi darò la pecora al calzolaio per avere la scarpa. Il che non è molto comodo: devo andare da quello che ha le pecore, che però capisce la mia necessità e mi dà solo una pecora per il mio asinello, invece di due. Così ho perso l’asino e mi trovo ad aver pagato un paio di scarpe un asino intero –l’equivalente di due pecore.

I prezzi sono viziati dalla difficoltà delle transazioni.

Come possiamo immaginarci l’introduzione della moneta in questo villaggio di pastori?

Immaginiamo che ci siano solamente cento pecore. Le transazioni avvengono con queste cento pecore.

Ma il capo villaggio ha un idea: emette moneta, e si fa garante di questa moneta. Ossia, dice: “Ragazzi, ogni moneta vale una pecora. Se voi venite da me con questa moneta e io vi do la pecora…”

Come quando negli anni settanta c’era scritto sulle banconote “Pagabile a vista al portatore”. Teoricamente andavi in banca centrale, e ti davano l’equivalente in oro. È una moneta convertibile. Stessa cosa con la moneta del nostro villaggio, la si può convertire in pecore.

Il capovillaggio emette le monete, la gente si scambia queste monete sapendo che valgono una pecora. Quando uno ha fame, ma ha solo una moneta, va dal capo villaggio che, con le tasse o altri mezzi, recupera una pecora e gli dà una pecora per mangiare.

E con questo l’abbiamo inventato il capitalismo… originario.

Tralasciamo la parte negativa, ossia che qualche abitante del villaggio inizia ad accumulare monete, e considera le monete come un bene –e non come portatrici di bene. Continuiamo ad analizzare i possibili vantaggi.

Il nostro capo villaggio, dopo avere emesso cento monete in cui ogni moneta vale una pecora, vorrebbe migliorare la vita dei propri concittadini. Vorrebbe inventare qualcosa per produrre più cibo, e gli viene un’idea. Ci sono delle persone –i creativi gli scienziati– che se ne stanno lì sotto un albero, a parlare, parlare… non fanno altro che immaginarsi grandi miglioramenti sociali, che ahinoi non riescono a realizzare perché nessuno vuole dare loro un po’ di monete senza nulla in cambio.

Allora cosa fa questo capo villaggio? Emette altre 100 monete. Quindi crea 100 monete. Crea della ricchezza? No, non ha creato dalla ricchezza perché la ricchezza abbiamo detto sono solamente le pecore — in questo villaggio la gente mangia solo pecore.

Quindi vuol dire che, dopo la nuova emissione, abbiamo 200 monete e cento pecore. Ossia ogni moneta vale solo mezza pecora. Ma c’è, come dire, un periodo in cui nessuno si accorge di questa “svalutazione” della moneta. Non è che tutti vanno subito a convertire queste monete in pecore. e quindi c’è un momento di esuberanza. Tutti quanti si pensano un po’ più ricchi, compresi questi filosofi che si sono ritrovati delle monete per fare ricerca e sviluppo, e che si mettono lì, lavorano, comprano un po’ di materiali per fare esperimenti, e inventano l’agricoltura!

Così l’anno dopo, dopo un ciclo economico, questo villaggio non ha più solamente cento pecore: ha cento pecore e 100 quintali di grano –perché ha inventato l’agricoltura.

Il paese, il villaggio, è diventato molto più ricco. Il capo villaggio ha fatto un un trucchetto: ha anticipato della ricchezza all’industria, agli scienziati, che hanno fatto ricerca e sviluppo, e adesso una moneta vale o una pecora oppure un quintale di grano, e ci sono 200 monete, non più solo 100! Con la liquidità finanziaria iniziale ha creato della ricchezza.

Questo, semplificando, è quello che sta succedendo adesso.

Il primo step è maggiore liquidità e quindi anche prezzi migliori. Pensiamo che un mercato poco liquido come quello dell’immobiliare ha un costo di transazione del 6 per cento, e infatti i prezzi sono alti rispetto al costo di produzione, proprio perché il mercato è molto illiquido. Quindi: più liquidità, prezzi più bassi.

Ma adesso, in questo momento storico abbiamo anche il secondo aspetto –quello del capo del villaggio che immette denaro: abbiamo le banche centrali che stanno continuando a mettere soldi nel sistema. Quello che ci si potrebbe aspettare è la prima fase –che il denaro valga sempre meno, che ci sia svalutazione della moneta.

Solo che questa cosa non sta avvenendo! Abbiamo le banche centrali che ormai dalla crisi del 2008 continuano a immettere nel sistema sempre più denaro senza che si veda un aumento dei prezzi. Che è una cosa abbastanza strana… evidentemente abbiamo inventato una nuova agricoltura!

Cos’è che rappresenta… cos’è il grano di oggi?

Il grano di oggi è un grano digitale: è il computer.

Il computer non solamente ci può servire per comunicare –cosa che ovviamente aumenta la produttività: prima dovevamo viaggiare per poterci parlare in faccia… adesso, sì sarebbe bello potersi parlare in faccia, però abbiamo avuto quasi un anno di lockdown, e moltissime persone hanno continuato a lavorare grazie al computer, cosa che non sarebbe stata possibile solamente 20 anni fa.

Ma abbiamo il computer che, in realtà, ottimizza buona parte dei nostri processi produttivi: dalla produzione agricola a quella industriale, fino ai servizi. Stiamo entrando, insomma, in un’economia di massima efficienza grazie al fatto che tutta l’informazione, piano piano, viene distribuita in questo unico cervello attorno al globo. E questo cervello elettronico gestisce, per noi, la produzione e la distribuzione dei beni.

Come abbiamo fatto per la nascita del capitalismo, tralasciamo i possibili scenari distopici –col computer che prende il potere e ci rende suoi schiavi. Guardiamo a qualcosa che, al momento, distopico non è –l’andamento delle borse.

Una cosa che stupisce gli analisti oggigiorno è che, come abbiamo già detto altre volte, le società, le aziende, sembra sembrano essere sopravvalutate rispetto a quello che producono.

Continuano ad arrivargli tanti soldi dagli investitori. Perché? Perché comunque le banche centrali stanno immettendo soldi nel sistema,
il sistema non sa bene dove investire perché tutto ciò che è a basso rischio
ha un rendimento pari a zero o addirittura negativo: se uno prova ad investire, appunto, dando soldi alla banca, la banca gliene dà indietro ancora di meno.

E quindi cosa fanno gli investitori? Investono in borsa.

Poiché se tanta gente vuole comprare le azioni di una società, le azioni di questa società vanno su, gli investitori per ora stanno guadagnando bene. Questo è un aspetto positivo, ovviamente, per chi investe in borsa. E tra l’altro in un altro articolo dell’Economist, sempre questa settimana, si riporta che il numero di retail investor è aumentato nel 2020 dal 10 al 25 per cento.

Purtroppo, per chi per esempio mette su una start up forse non è necessariamente una cosa buona. Le startup possono essere più… disruptive, innovativa, di una grande azienda, ma, soprattutto in Italia, non trovano soldi. E non trovano soldi, ancora: soprattutto in Italia, perché la banca non vuole prestare i soldi al piccolo imprenditore che sta mettendo su… un’azienda.

Alla fine alla banca conviene investire nel mercato azionario. Il rapporto guadagno su rischio è sicuramente maggiore rispetto all’investimento sul piccolo imprenditore, che invece –soprattutto in Italia!– tra balzelli e vari problemi burocratici ha una maggiore possibilità probabilità di fallire.

di Mario Alemi e Alessandro Simonetti (trascrizione del video).

https://medium.com/media/e511b67d6db79530dada3c1991e49076/href

Oggi commentiamo un articolo dal titolo “Why you should ignore the siren call of market timing”. L’articolo inizia con una citazione di un intrattenitore americano che dice “Bisognerebbe comprare le azioni quando stanno per salire mentre bisognerebbe venderle quando stanno scendendo”. Facile a dirsi dice Paul Samuelson, uno dei più famosi importanti economisti del novecento…

Due parole su Samuelson. È un mostro della dell’economia e della finanza, e nel novecento è colui che in un certo senso ha introdotto la matematica dura e pura in economia. Samuelson si laurea a Harvard e poi va all’MIT, anche perché Harvard era “un po’ antisemita”, e non l’avrebbe mai preso. Va all’MIT (Massachusetts Institute of Technology) dove ci sono matematici, fisici, ingegneri e dove, pur essendo economista, si trovava a subito a suo agio.

Lì inizia a lavorare sulla teoria il più matematica possibile dell’economia e della finanza. Ora, non che gli economisti prima di Samuelson non ne capissero di matematica –pensiamo a “I manoscritti matematici”, di Karl Marx, che pur essendo laureato in legge, di matematica qualcosa ne capiva, a Keynes che ha scritto dei trattati di statistica… ovviamente gli economisti tipicamente sono dei buoni matematici. Però qua parliamo anche di qualcosa forse di un po’ più filosofico. Samuelson era anche un ottimo filosofo, qualcuno che riusciva a dimostrare anche con la logica, con la retorica, la dialettica, alcune sue idee.

Quindi per Samuelson è impossibile predire se le azioni saliranno e scenderanno perché se così fosse allora tutti comprerebbero e venderebbero nel momento giusto, nel momento che è stato predetto. Nessuno ci guadagnerebbe perché tu ci guadagni se compri prima degli altri.

Che non ci si possa guadagnare è alla base della finanza. Cioè l’idea che i prezzi di mercato seguono un andamento caotico, random, casuale…
Io non so come esattamente delle azioni andranno, se saranno apprezzate domani.

L’idea che i prezzi seguano un andamento casuale nasce nel novecento grazie a un matematico francese, Luis Bachelier, che analizzò quest’ipotesi nella sua tesi di dottorato, nel 1900, “Sulla teoria della speculazione”. Ipotesi che poi va avanti, si sviluppa fino agli anni 70…

Come referenza: “The Random Character of Stock Market Prices”, un libro edito da Paul Cootner, nel 1964, che raccoglie tutti gli articoli che studiano la caratteristica casuale del mercato che dicono in pratica è impossibile guadagnare comprando e vendendo velocemente sul mercato. È impossibile che qualcuno riesca a capire l’andamento del mercato in maniera più intelligente gli altri.

Secondo Samuelson, ma non solo, il fatto che non si possa conoscere con certezza l’andamento del mercato –non si possa predire l’andamento del mercato– è un po’ come nella meccanica quantistica in cui non si può identificare la posizione di un elettrone nello spazio.

In fisica c’è il principio d’indeterminazione di Heisenberg che dice non possiamo sapere con assoluta precisione la posizione di un elettrone.
In finanza cioè l’ipotesi del mercato efficiente. Cosa vuol dire? Abbiamo tutti quanti accesso alla stessa quantità e qualità di informazione. Quindi se in un’azione da un po’ su o un po’ giù — un po’ più su di quello che il mercato si aspetta– in realtà è perché è successo qualcosa di casuale… come un po’ più di gente, che so, ha ricevuto un po’ di eredità, ha ricevuto po’ di soldi e quindi investe un po’ di più e questa azione va un po’ più su.

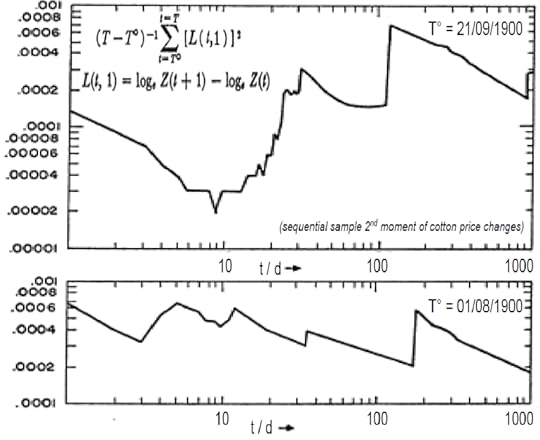
Immagine dall’articolo di Mandelbrot “The Variation of Certain Speculative Prices”.

Poi altrettanto casualmente andrà un po’ giù perché per caso la maggioranza di investitori ha dovuto vendere un po’ più giù. Ma non è prevedibile questo piccolo spostamento dalla traiettoria in su o in giù. È totalmente è casuale. E infatti si chiama random walk –un cammino casuale.

L’azione in realtà sta andando, immaginiamo, su in maniera lineare e ma si muove casualmente attorno a questa questa curva ideale. E questo andamento attorno alla curva ideale è totalmente random e non è prevedibile.

Eppure però c’è anche chi guadagna…

Viene in mente la fine di “Io e Annie” di Woody Allen, in cui parlando dell’amore… Esiste o no l’amore? Ci devi credere che esiste. Una volta che ci credi, l’amore effettivamente esiste. E Woody Allen prende l’esempio di uno che va dallo psichiatra e dice “Dottore dottore mio fratello è totalmente folle: crede di essere una gallina.” E il dottore dice “Inizi a portarlo in un ospedale psichiatrico”. “E poi l’ovetto la mattina e chi me lo fa?”.

Certe volte, essendo pazzi, non si sa che si stanno facendo delle cose impossibili.

I matematici probabilmente sono un po’ pazzi, quindi non sapendo della dell’efficienza totale del mercato riescono a fare l’impossibile, che è guadagnare un sacco di soldi applicando delle formule che possono predire l’andamento del mercato.

Quindi esiste la possibilità di predire l’andamento dei prezzi?

C’è la leggenda di Eulero, il principe dei matematici, che pur guadagnando mille taglieri l’anno lascia un’eredità di 37 mila talleri, semplicemente investendo. C’è la leggenda di Gauss che ha lasciato un sacco di talleri anche lui, morendo. (C’è anche la leggenda di Newton che invece ha perso l’equivalente di 3 milioni di euro odierni e dice “È più facile prevedere l’andamento dei pianeti che la pazzia delle menti umane”). Però c’è la realtà dei matematici del novecento che sono veramente diventati i ricchi con il mercato azionario.

Uno è un po’ il padre del digitale, Claude Shannon. La volta scorsa aveva parlato di chip, avevamo detto che il chip ragionano con la logica “vero-falso”, mettono dentro degli “zero” e “uno”, ecco, la mente che ha inventato tutto questo si chiama Claude Shannon, che nella sua tesi di Master, a 20 anni dimostra che è possibile avere dei circuiti elettrici che calcolano immagazzinando nei circuiti elettrici gli zero e gli uno.

Claude Shannon non si sa quanto abbiamo guadagnato, ma ha sicuramente guadagnato, e ha sempre detto facendo dei modelli matematici che prevedevano l’andamento dei prezzi del mercato.

Vicino a Claude Shannon c’è un suo compagno di avventura, più giovane. Il matematico e fisico Edward Thorp, che non solo ha inventato il metodo per vincere a blackjack, e inizia in realtà con “How to beat the dealer”… inizia vincendo il banco nei casinò finché non lo sbattono fuori e non lo fanno più entrare in nessun casinò.
Ma poi continua vincendo il mercato. Quindi lavora a delle formule, ovviamente utilizzando il computer, per poter guadagnare consistentemente investendo sul mercato.

E non ci sono dubbi: Edward Thorp ha sempre guadagnato applicando delle formule matematiche.

E poi c’è quello che in un articolo dell’economist di qualche mese fa viene definito un tirannosauro rex. Dice “Se io mi trovassi in cortile –parla non so quale gestore di fondi– mi trovassi nel mio cortile un leone rimarrei molto sorpreso. Ma esiste un fondo di investimento che non è l’equivalente di un leone del mio giardino d’inverno. È l’equivalente di un tirannosauro rex nel mio giardino. Cioè qualcosa che non posso neanche immaginare. Non è possibile.”

Qui parliamo della Renaissance Technology. Un fondo di investimento fondato da Jim Simons, un matematico, anche molto bravo, che però ha sempre desiderato fare cose un po’ diverse. A un certo punto si è scocciato di lavorare in università, ha preso i soldi di suo padre e ha cominciato a investire, a detta sua senza nessuna formula, cercando di fare i migliori investimenti che gli venivano in mente.

Sempre a detta sua, all’inizio, gli è andata bene per pura fortuna. Simons riconosce che all’inizio ha guadagnato per caso, come come fanno molte persone che guadagnano investendo, facendo trading sul mercato: è solamente per pura fortuna… ma ad un certo punto gli è venuto in mente che poteva applicare alcune alcune branche della matematica di cui lui era un profondo conoscitore per poter prevedere l’andamento dei prezzi del mercato. Che è quello esattamente di cui l’economist si prende gioco nell’articolo. Sapere quando un’azione salirà e sapere quando un’azione scenderà. Se so che salirà la compro prima se so che scenderà la vendo prima che scenda.

Ecco, Simons praticamente inizia a lavorare con un collega ad un modello matematico che sembra funzionare. Negli anni ‘80 fonda il fondo medaglione, Medallion Fund, che praticamente dalla fine degli anni ’80, ogni singolo anno, guadagna il 60 per cento. Ha due particolarità. 1) è un fondo chiuso, dove non è che io e te possiamo mettere i soldi 2) è un fondo in cui quelli che ci stanno dentro si devono prendere questo 60 per cento, non possono tenerlo dentro perché se no adesso sarebbe così grande che sarebbe l’unico giocatore all’interno del mercato. Quindi quei miliardi investiti –mettiamo 10 miliardi ogni anno– producono 6 miliardi quasi 6 miliardi vengono tirati fuori.

Simons si stima che abbia una dozzina di miliardi di euro cash suoi, e in realtà sembra un po’ dare torto all’ipotesi del mercato efficiente, dall’altra parte sembra dare ragione, nel senso che è veramente l’unico con un rendimento così alto.

Ma attenzione. Il consiglio che dà Simons non è quello di studiare matematica anche perché obiettivamente il livello della matematica di Simons è molto avanzato. Non sono non ce ne sono tanti al mondo che fanno la matematica. Il consiglio che dà Simons, che lui dice essere la chiave del successo del suo fondo è quello di prendere persone brave, intelligenti, possibilmente più intelligente di te, e di farle lavorare di libertà, di farle comunicare tra di loro.

Il segreto del Medallion Fund non è quello di aver avuto alla base un Simons che ha creato la formula magica ma di aver avuto un centinaio di persone estremamente intelligenti che lavorando insieme hanno tirato fuori qualcosa di super valido. Ma soprattutto, dice Simons, non è che io le ho assunte. Le ho messe là dentro e gli ho dato una parte del fondo.

Tutti i matematici potrebbero diventare ricchi o comunque sia potrebbero avere successo nel mondo della finanza? Probabilmente sì però c’è anche da dire che alla maggior parte dei matematici in realtà non gliene frega niente di diventare ricchi.

Probabilmente ancora più famoso di Jim Simons è Grigori Perelman che è matematico che studia esattamente la stessa cosa di Simons, cioè la geometria differenziale, che però dimostra il teorema più difficile in geometria differenziale –comunque uno dei problemi più difficili in matematica. La congettura di Poincaré. La dimostrazione della congettura di Poincaré viene premiata con un milione di dollari più la medaglia Fields, che è ancor più del premio Nobel per la matematica (solo ogni quattro anni solamente a gente con meno di 40 anni, quindi veramente un riconoscimento…. incredibilmente straordinario).

Bene, Perelman rifiuta sia il milione di dollari sia la medaglia Fields. Si ritira a San Pietroburgo, vive con la mamma e rifiuta non solo i riconoscimenti, ma anche le offerte di lavoro, rifiuta tutto per una vita di riservatezza. Gli basta, forse, godere le vette matematiche che è riuscito a raggiungere.

In conclusione, conviene investire solo se siamo in grado di predire oppure non conviene mai?

Diciamo una persona che ha investito nel 2008 adesso ha guadagnato… molto. Per cui, col senno di poi, sicuramente sarebbe stato bene investire: i mercati sono in crescita da da più di dieci anni.

Un ottimo consiglio ce lo da Samuelson: non investire mai più di quello che ci sentiamo tranquilli di poter investire. Investiamo sempre qualcosa che possiamo immaginare potremmo perdere da un momento all’altro.

In più, aggiungiamo noi, c’è chi può prevedere e chi non può prevedere. Noi tutti sicuramente siamo tra le persone che non possono prevedere l’andamento di mercato. Gente con la testa di Gauss, Eulero, Shannon, Thorp o Simons… sì: probabilmente loro possono prevedere il mercato.

Back in the 1990s, Google’s business model was selling private search engines to companies for their intranet. They soon discovered it didn’t work. Google’s original algorithm was measuring how important a page was by looking at the centrality of that page in the network of the world wide web –roughly, how many links were pointing to that page, and to the pages pointing to that page, and so on.

In an intranet, such information is useless: the network of web-pages is small and with very people creating links to pages they think are interesting and valid.

Why was Google computing the centrality? Because the centrality of a node in a network can be seen as the number of times the node is visited by a random surfer. And this information tells you how important the page is.

How was the centrality computed? Imagine you are in a page with 4 links. You produce a random number between 1 and 4 which tells you where to go next. In the new page you’ll do the same, and so on. The more often you’ll visit that page, the higher the centrality of the page.

Because surfer in an intranet do not surf at random, but usually look for specific information, measuring the centrality of a page tells little about that page. In addition, we don’t really need to compute such information, because we have it: for each page, we know how often, and for how long, our surfers visit it. We can therefore use the actual number of visits to the page instead of the estimated number through the centrality.

This can help us provide better results. If a user search for “How to esign” and there are only pages about “How to resign” and “How to design”, both pages are equally good candidates. But if the first is visited only 20 times a year and the second 10,000 times, any good algorithm should provide the page about “design” as the best candidate.

Let’s visualise the space of probability of a search:

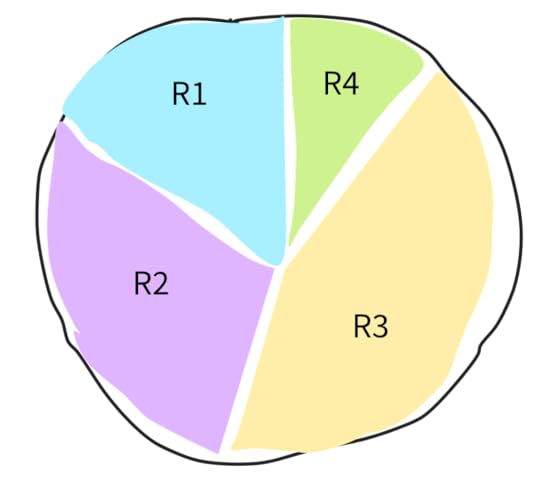The black circle is the space of probability of the pages.Each section inside the circle represent a possible result: the bigger the section, the higher the probability that a random user (e.g. someone throwing darts) choses that page.

With a query, the user will filter out a region of the search space, but for the moment let’s focus on the size of the sectors in the probability space.

We want to compute a probability distribution function (PDF) for the likelihood that page R might be the desired page when the user didn’t provide any search query. Something like “How likely this page would interest someone who stumbles upon my website?”. And we want to use previous visits as a proxy to compute this likelihood. We call that:

P(r|{n, N}) = likelihood that page R elicits an interest of value r , computed from having observed in the past n visits to that page out of N total visits to the website.

We cannot use a simple proxy as

P(r|{n, N}) = n/N

because this would mean that a page which has never been visited could never be found interesting.

To compute our likelihood, we start with the Bayes formula:

P(r|{n, N}) ∝ P({n, N}|r) •P(r)

It says that the likelihood of R being of interest r is proportional to the probability of observing n and N given that the a priori interest in that page is r.

The value of P(r) is –if we do not make assumption like “The company is on the verge on bankruptcy and people will look for How to resign even if the page was seldom visited in the past”– a uniform function between 0 and 1. The page, as far as we know, might be very interesting or of no interest at all –we don’t know, and that’s why we are going to look at previous visits.

P({n, N}|r) is more interesting. The probability of observing n successes given N trials is give by the binomial distribution, i.e.

P({n, N}|r) ∝ rⁿ•(1-r)⁽ᴺ⁻ⁿ⁾

Note that if n=0, i.e. the page is never visited, the PDF becomes (1-r)ᴺ, something like that:

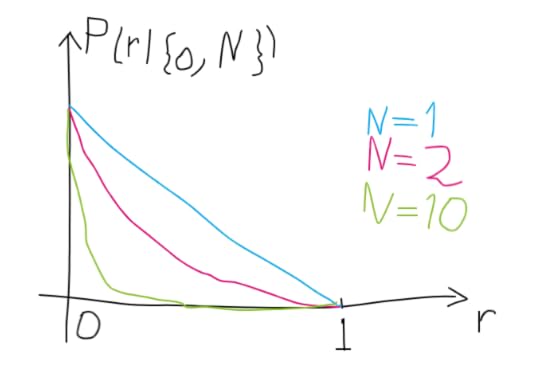
That means that we are more and more confident that the page is not interesting when more visitors never visit it.

In general, the more the data, the higher our confidence. If the page is visited 8 times out of 10, or 80 times out of 100, we get increasingly more confident about the page having an interest of 0.8:

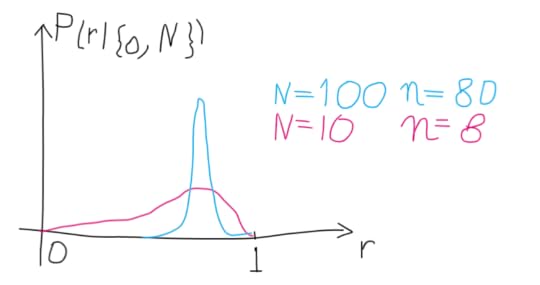
The PDF of our page eliciting an interest of value r , given the observed visits, is:

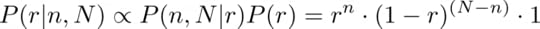
Although we could use the PDF for computing the final score to give to the page, better to compute now the expected value of the interest r given the visits:

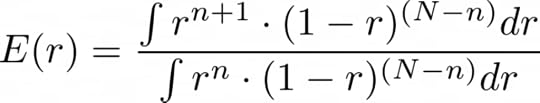
The denominator is not necessary (the PDF is not normalised anyway), but it will be useful later for simplifying the result. The indefinite integral of the numerator solves to:

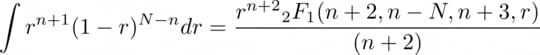
Where 2F1 is the hypergeometric functions. But we are actually interested in the definite integral, and luckily, WolframAlpha also helps us compute the numerator…

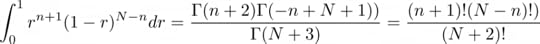
…and the denominator:

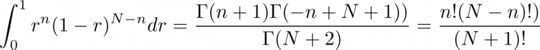
Which finally gives us:

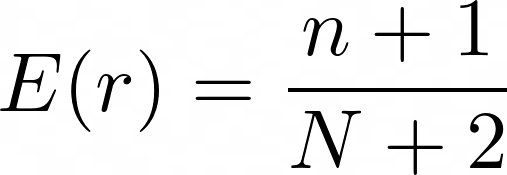
Admittedly that’s a simpler result one would expect after the initial integral, but a very sensible one: for good statistical samples the expected interest r grows like n/N. But as long as we only have very few counts, all pages are, in practice, equally important.

Note that one could say: “A single visit says little about the validity of the page. Unless we have 100s of visits for a page, I don’t want to favour this page against the others.” This would be an antidote against the Matthew principle (the rich gets richer), which favours pages that, maybe by chance, started with more visits than others. In this case we can transform the value to:

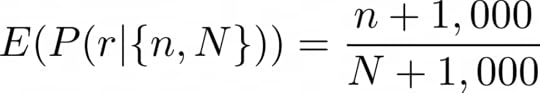
In this way, if I have 100 pages where 99 received no visits and one received 100 visits, the (not normalised) expected desire for the latter is 1,100/1,100=1, while for the former ones is 1,000/1,100=0.9. Or I could counteract the emerging power law in the number of visits taking log(n) and log(N).

Using the User’s Query

Now we want to compute the likelihood that a page is the desired one given a user’s query.

For that, we will use the concept of distance between the query and the page. Because all pages are different, they have distance d > 0 between themselves.

While a distance has no upper bound, in our case it would be good to have something bounded, e.g. cosine distance, which provides values in [-1, 1]. Once we have that, we can normalize it to [0, 1] and define similarity s as:

s = 1– d

The similarity s goes ideally from 0 (nothing in common) to 1 (the Query coincides with the page).

Finally, we can save that the probability that a page R is the desired one, given a similarity s between the query and the page and n visits to the page out of a total N:

P(R|s, {n, N}) ∝ P(s|R, {n, N})•P(R, {n, N})

P(s) does not depend on neither n nor N. In addition, for what we know, the probability that a user writes a query of similarity s to a page if they want that page is… s itself. If the user wants a page about resignation will write something as similar as possible to “resignation”.

Therefore, the last formula translates to:

P(R|s, {n, N}) ∝ s • (n+1)

Note that it would be nice if the pages were a basis in the space where we represent the query: in this case we could use the component of the normalised query with each basis (page) as similarity.

In this case, if a page has similarity s=1 (i.e. distance =0) with the query, it will be the only choice, because all the others will have similarity 0. Otherwise the likelihood that it’s the right one is proportional to similarity to the query times the number of visits n+1.

Because pages are not orthogonal between each other, it’s important to exclude all pages which we believe are not requested by the user. For instance, in case we use n-gram cosine similarity, we can take only pages with a similarity bigger than 0.8, and only then multiply by n+1.

Using Logarithms

As quickly written above, one could consider using log(n) instead of n.

The reasoning behind is that the ranking of pages by popularity follows a power law –kind of:

1ˢᵗ page visits = nₒ
2ⁿᵈ page visits = nₒ/2
3ʳᵈ page visits = nₒ/3
…

or:

n = nₒ / R => log(n) = log(nₒ)–log(R)

That means that for a page to become more popular (wanted) than another page, it must increase its visits by an order of magnitude. What matters in page visits (or product sales) is not the actual number, but the logarithm of it. It’s like for money: if your income is €10,000 a year, you would be happy with a €10,000 increase. If your income is €1M, €10,000 would mean close to nothing.

Therefore, although the probability of being chosen goes with n –which makes sense– the importance of a page does not go with n, but with the logarithm of it. Therefore we can rewrite our search formula with:

search score = s • log(n + 2)

L'Economist della Settimana

L’articolo di Johnson (il “linguista” dell’Economist) del 17 ottobre questa settimana si sofferma su un interrogativo apparentemente fazioso: il fatto di saper identificare l’aroma di un vino con un nome, mi permette di percepire meglio questo aroma?

La stessa domanda ritorna nei più svariati campi. Dalla moda alla matematica.

Il fatto che una sciura possa saper descrivere decine di colori, i colori che ritrovano nei suoi vestiti, mentre il gandula sappia a malapena riconoscere gli otto colori delle matite colorate della sua infanzia, vuol dire che i due percepiscono in maniera diversa i colori?

Per dirla con Wittgenstein, e qui passiamo dalla moda alla filosofia, i limiti del mio linguaggio definiscono i limiti del mio pensiero?

E divertente leggere in questo pezzo come il problema del limite del pensiero del linguaggio, un problema squisitamente di inizio novecento, sia oggi affrontato in maniera quasi goliardica -e con successo.

Gli esperimenti fatti con i sommelier hanno dimostrato che no, i limiti del linguaggio non sono i limiti del pensiero. Possiamo sapere identificare un aroma, senza per questo saperlo definire verbalmente.

Per esempio, posso stappare una bottiglia di Café 124, annusarla, chiudere gli occhi, non dire nulla, e comunque percepirne tutta la ricchezza aromatica.

Come canta Paolo Conte. “Complesso è questo aroma che ha il caffè, opaco e scintillante ma ormai in te”

Adesso, uno può pensare che queste ricerche siano leziose, invece sono alla base della logica, e quindi anche dell’informatica. Il ruolo del linguaggio nella logica ed in matematica è stato investigato profondamente all’inizio del 900 – Bourbaki, Wittgenstein per l’appunto, Hadamard, Hilbert, Peano, Bertrand Russel e Whitehead… Tutti i filosofi che hanno ricercato un linguaggio che potesse, si sperava, definire un costrutto logicamente perfetto, E quindi una matematica più potente.

Ma si scopre poi, con Gödel, che è impossibile costruire una logica priva di contraddizioni. Quale che sia il linguaggio usato. Comunque, l’importanza che noi diamo al linguaggio non per questo è diminuita. Solo si è spostata su un altro piano. Abbiamo infatti capito che linguaggio è importante non solo, o non tanto, per aiutarci a capire, ma soprattutto per far capire. Se anche uno scimpanzé sente l’aroma del caffè come complesso, opaco e scintillante, difficilmente può comunicarlo ad altri.

Il linguaggio è, udite udite, alla base della comunicazione, non della comprensione. Chi l’avrebbe detto.

Per dirla con Newton, il linguaggio ci permette di costruire sulle spalle dei giganti. I giganti del passato. Se Newton non avesse potuto leggere Galileo, gli sarebbe mancata una spalla importante su cui poter lavorare. Il linguaggio è la scala che ci permette di salire sulle spalle dei giganti.

Tornando al ludico, se Claude Shannon, uno dei padri dell’informatica moderna nonché esperto giocoliere, non avesse inventato un linguaggio per descrivere le figure del juggling, della giocoleria, ossia del mandare in aria degli oggetti e riprenderli con le mani descrivendo nell’aria complicate figure, le performance dei giocolieri sarebbero meno complesse. Un pensiero per Shannon ad ogni semaforo rosso con giocoliere.

Similmente saper scrivere la musica non vuol dire saper immaginare, comporre, una musica più complessa. Vuol dire principalmente avere un supporto mnemonico esterno che ci aiuta a rielaborare la composizione anche a mente fredda, una volta passata la scintilla creativa. E soprattutto di permettere anche ad altri di suonare la nostra musica, di studiarne in maniera approfondita la struttura, con calma.

Insomma il linguaggio è stato fondamentale sì per l’evoluzione della enologia e della caffetteria, ma anche della matematica, della musica, o della giocoleria.

https://www.economist.com/books-and-arts/2020/10/17/does-naming-a-thing-help-you-understand-it

Rare events are unpredictable

In 2008, during the credit crunch crisis, we heard people in finance saying “According to our model, something like that could happen only once in a billion years.” Clearly, the models had some problems.

Finance was mainly using so-called “value-at-risk” models to estimate the probability that assets’ value could drop below a certain threshold. But, as already pointed out by the Benoit Mandelbrot in 1963 (The Variation of certain speculative prices), prices of assets are not easy to predict.

Prices are like salaries –most of them are around a certain value, but some of them are shamefully high. You go to a meeting and normally suppose that no one is earning 1000 times as much as you do.

Nonetheless, even if you are a millionaire, you know that the probability of meeting a billionaire is low, but not zero. The exact probability would be hard to compute, but you know that betting your life on that would be risky… you know that the fact that you never met a billionaire in a meeting, does not make it impossible.

Prices are the same. You never saw in the past five years the S&P Index losing 30% of its value. But you know it can happen.

Many mathematical models, on the contrary, look at the past months/few years, and because they never see something happening conclude that it cannot happen.

Artificial Intelligence

Mind that those value-at-risk models are rational agents acting so to achieve –given observations and intrinsic uncertainties– the best expected outcomes. In other words, it’s Artificial Intelligence.

Although wrong (but of course any model is not perfect), value-at-risk models were useful. They allowed financial institution all over the world to analyse huge amount of data and to produce an estimate of what could have happened.

Maybe the real problem was that because of the (relative) mathematical complexity, and the staggering amount of data analysed, (almost) everyone in finance relied blindly to value-at-risk. In 2008, the Basel Committee on Banking Supervision still accepted it for modelling prices.

All that made banks under-estimating the probability of default for all the assets in their portfolio.

Deep Learning

Enters now Deep Learning, a branch of Artificial Intelligence. Instead of the prices of assets, today’s artificial neural-networks analyse written language, or videos, or audio, most of it produced during the past 20 years.

(Note that language shares many mathematical properties with prices and wages. Indeed, the same function was re-discovered many times to model wages (Pareto), frequency of words (Zipf) and prices (Mandelbrot).)

Neural networks, like value-at-risk, cannot imagine something new, outside the current paradigm. It never happens? It cannot happen. They merely look at the rear-view mirror, and, with a (relatively) complex mathematical model, predict the future.

But while humans know that the ways of Lord are infinite, software –which learns just from the statistics of the data it crunched– does not. For it, the ways of Lord are limited to the ones it has travelled.

If an airplane lands on the highway, humans understand what’s happening even if it’s the first time they see something similar. A neural network doesn’t, unless it’s been fed with that example. And the same goes for a cow on the road, or a bridge collapsing. Would you trust a self-driving car dealing with the road in front of you falling down?

Neural networks can ape human knowledge, but they are unable to understand, much less imagine, rare events –the black swans.

On the contrary, human beings, particularly the smart ones, are able to learn from unexpected events. To embed unexpected events in their ontological model, even if they have to change such model.

Alexander Fleming, the discoverer of penicillin, came back from his holidays and found a bacteria culture plate with an open lid. He observed that such plate had fewer bacteria than the others. He decided to investigate why the bacteria did not reproduce there, understood the cause, fought (as usual) with the establishment, and many years later humanity had a powerful antibiotic.

History of science is full of such anecdotes.

History of Artificial Intelligence is not, and never will. Imagine a neural network analysing Alexander Fleming’s samples:

Found plate with open lid.

Trash plate

Goodbye penicillin.

Le stime che trovate sotto si riferiscono ai dati di ospedalizzati con sintomi da COVID-19 nelle varie regioni italiane. I dati vengono forniti dalla protezione civile (https://github.com/pcm-dpc/COVID-19).

La ratio dietro alle previsioni è descritto in questo post, mentre il software sviluppato è disponibile qui: https://github.com/malemi/covid-19-prediction.

Come sempre, i dati non sono particolarmente puliti. Li ho “smussati” e ho preso solo gli ultimi 10 giorni, per rilevare ogni possibile cambiamento.

Direi che oramai non c’è più bisogno di fare previsioni, nel senso che avevamo previsto il 15 di marzo che a cavallo del mese la Lombardia avrebbe raggiunto il picco, cosa effettivamente accaduta.

Diversa la storia nelle altre regioni: chi viene ospedalizzato oggi è stato infettato 1–2 settimane fa. Per tutte le altre regioni veniva previsto un picco più alto e più tardi nel tempo, cosa che poi (come era stato detto) non è avvenuta. Si notava nelle previsioni che man mano che passavano i giorni i picchi si abbassavano e avvicinavano, segno che le misure di contenimento (iniziate verso l’8 marzo) stavano facendo effetto.

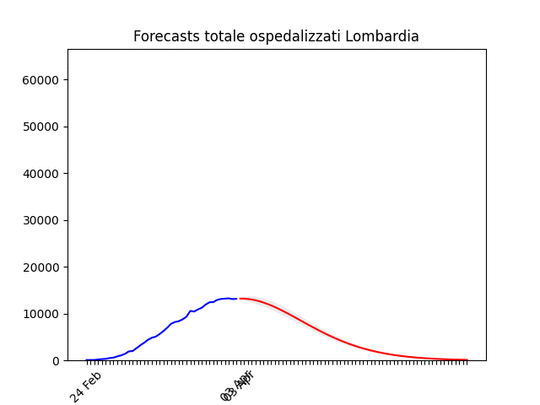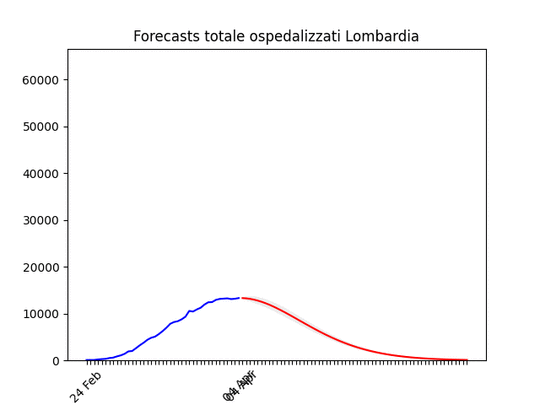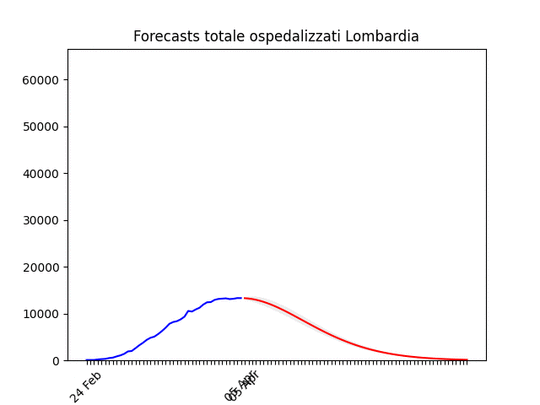Lombardia: Tutto come previsto. Notare che, dato l’elevato numero di ospedalizzati che ha saturato il sistema, è probabile che invece di un “picco” ci si trovi un “plateau”, ossia una zona piatta che durerà qualche giorno per poi iniziare a scendere.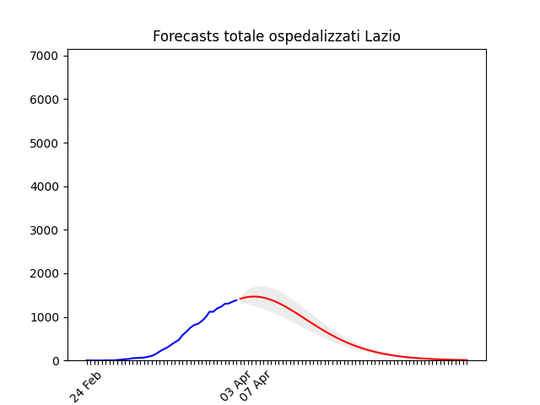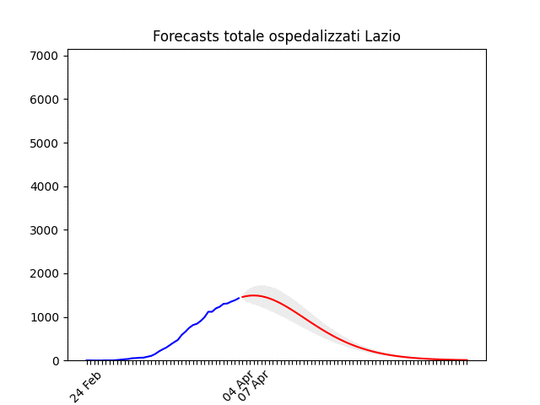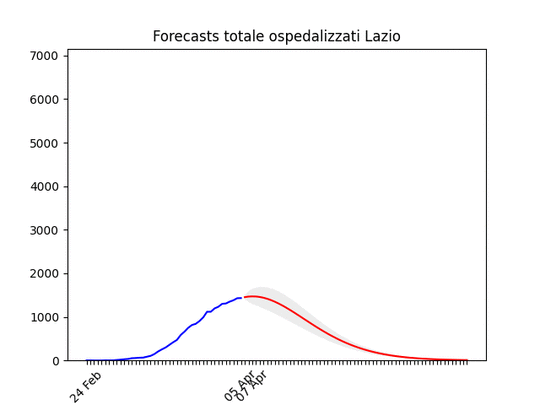Lazio: alla fine un numero elevato di ospedalizzati, ma non dovrebbe aumentare ulteriormente.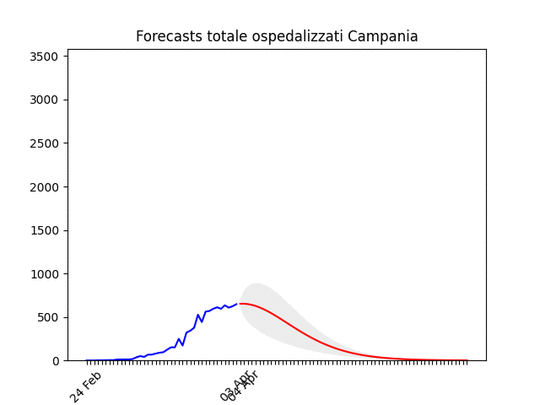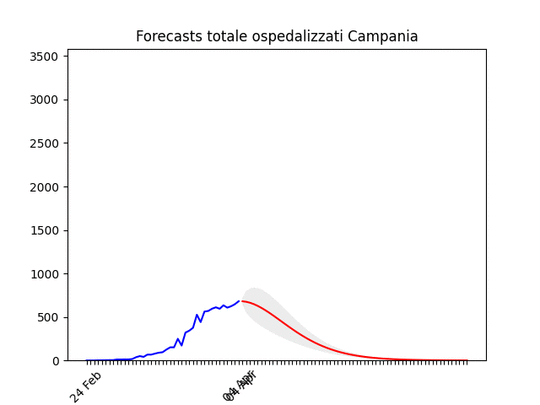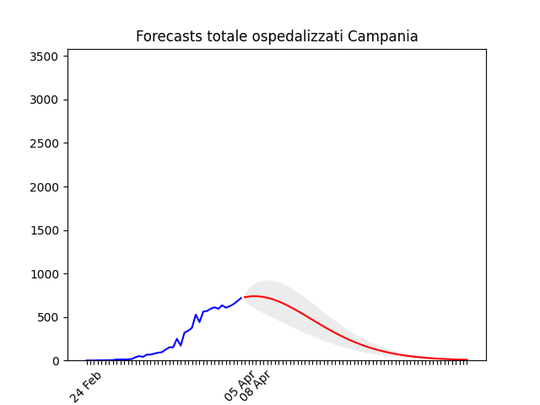Campania: Dati come sempre poco affidabili… ma sembra andare per il meglio.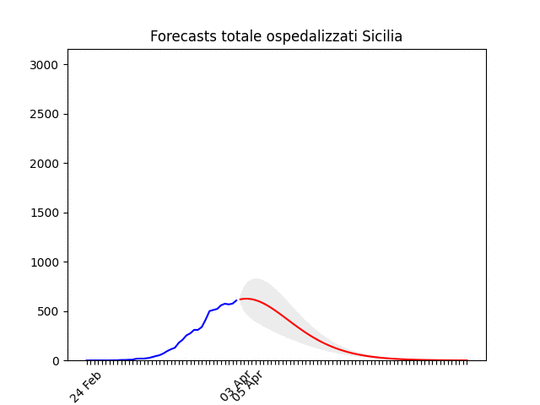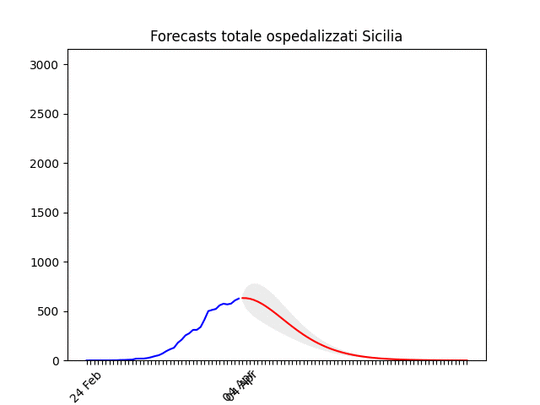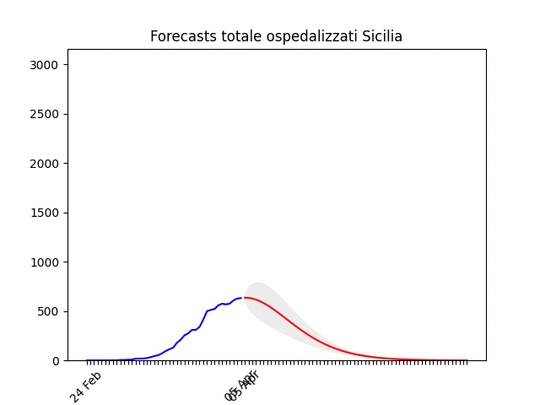Sicilia: anche qui dati non perfetti… ma ci siamo.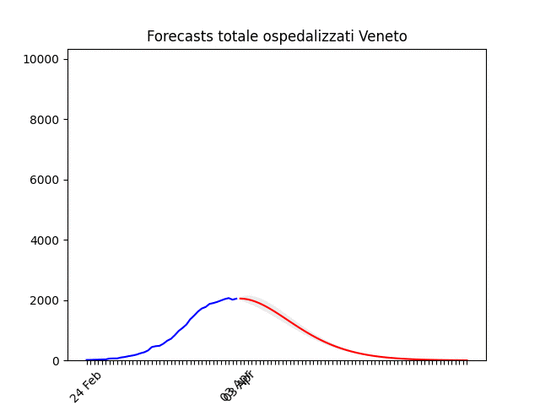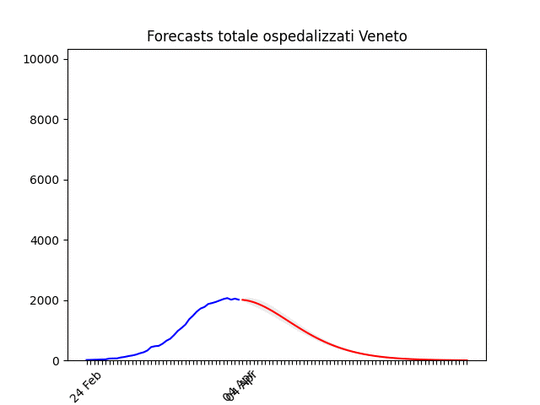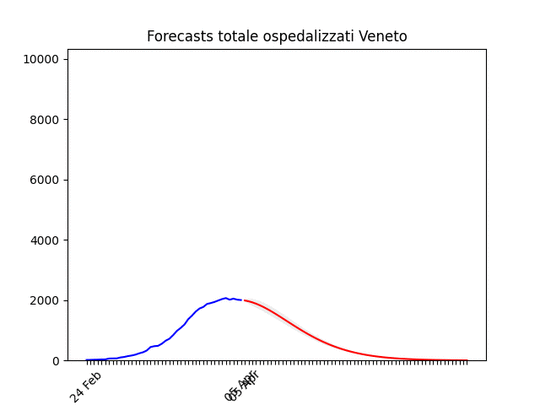Veneto: oltre il massimo.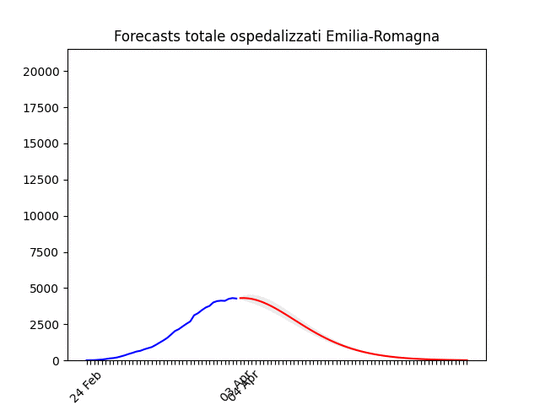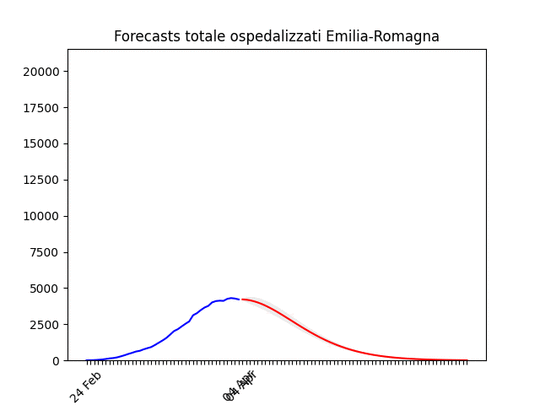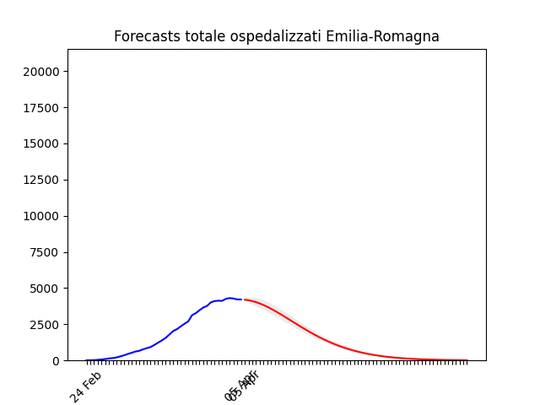Emilia-Romagna: decisamente oltre il picco.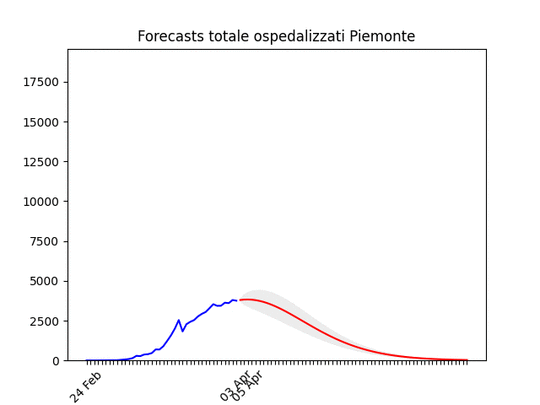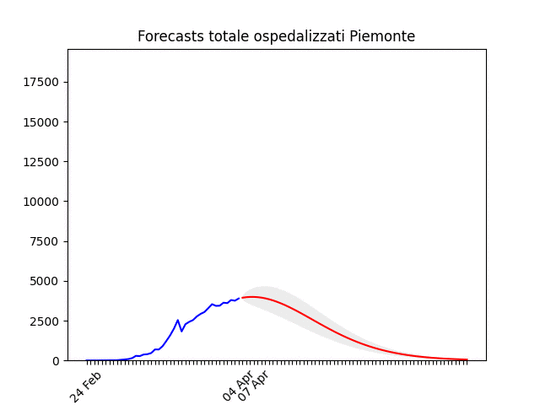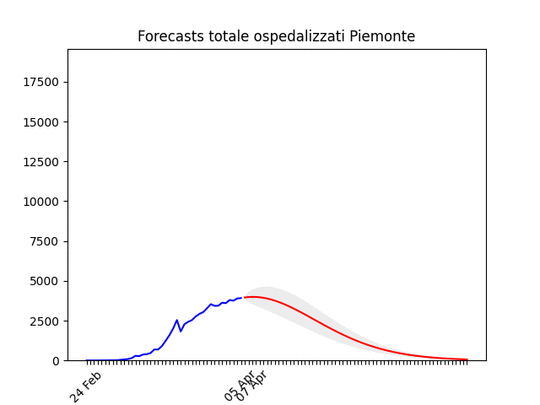Piemonte: continua con un andamento strano, ma sembra dover diminuire tra poco.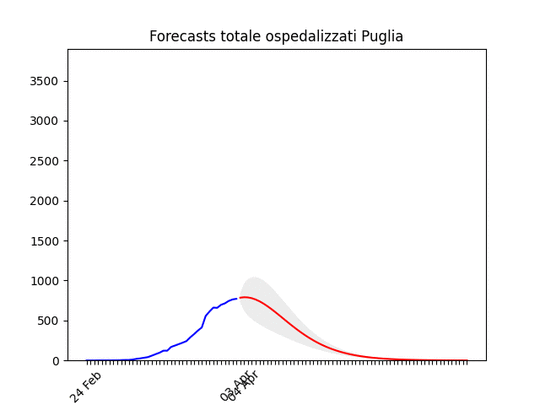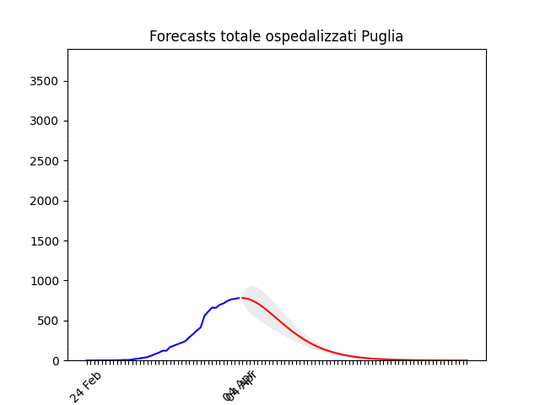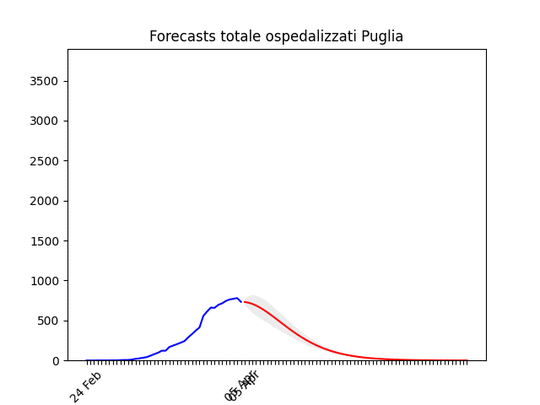Puglia: Dopo un aumento preoccupante sembra essersi stabilizzata e scendere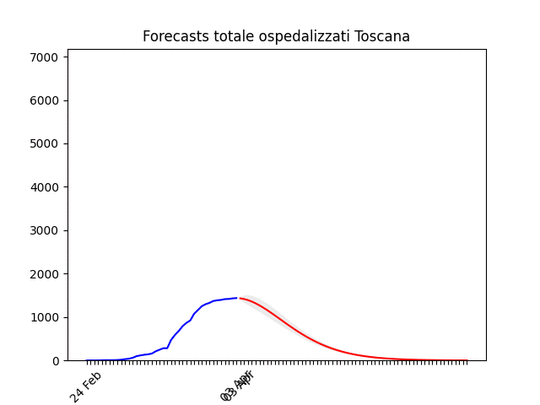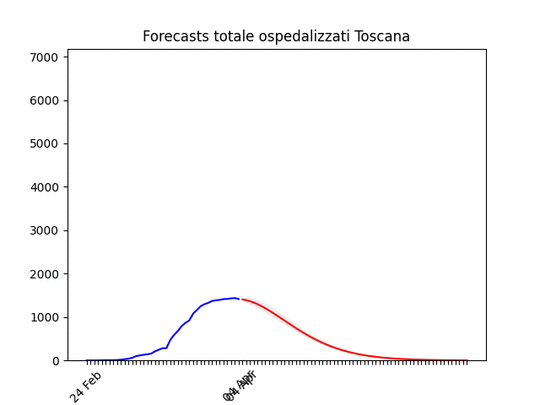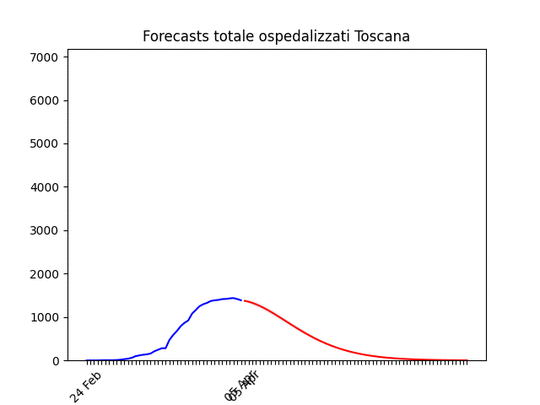Toscana: come sopra.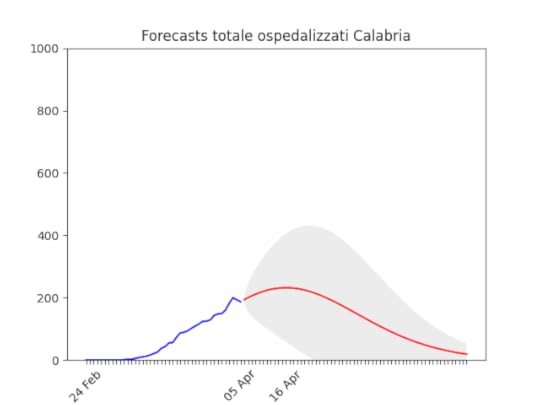Notare che la zona grigia (che indica l’incertezza, ossia il possibile errore) è enorme. La causa ovviamente è la curva a zig-zag negli ultimi giorni. In pratica l’algoritmo non capisce, ma direi che comunque la curva tende anche qui verso il basso.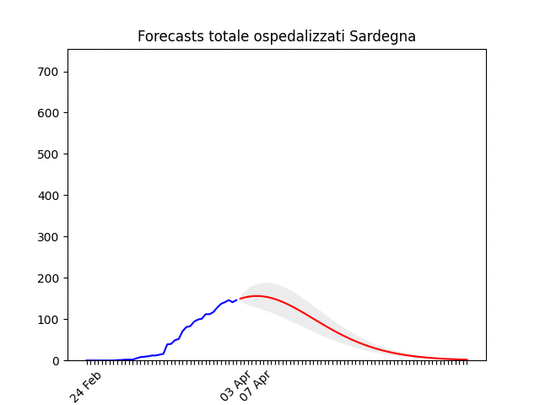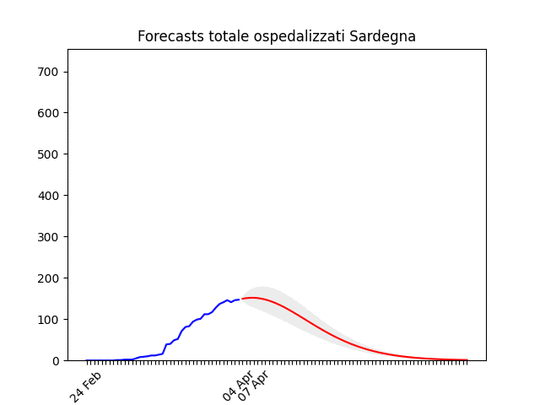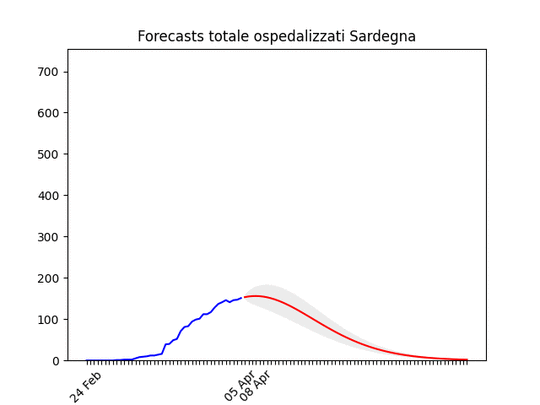Sardegna: La statistica (per fortuna) resta bassissima ma conferma uno scollinamento.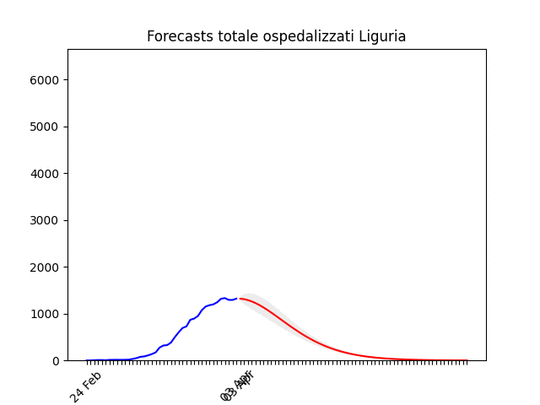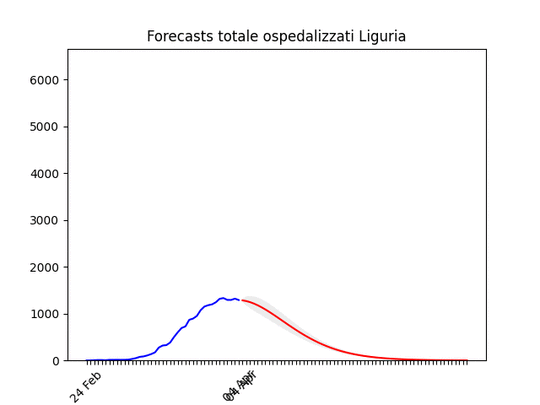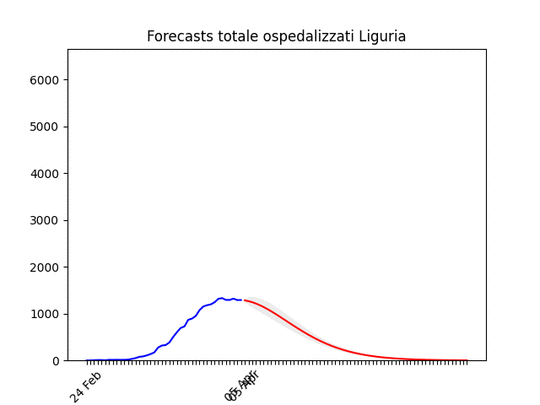Liguria: Numero di ospedalizzati alla fine alto, ma in discesa.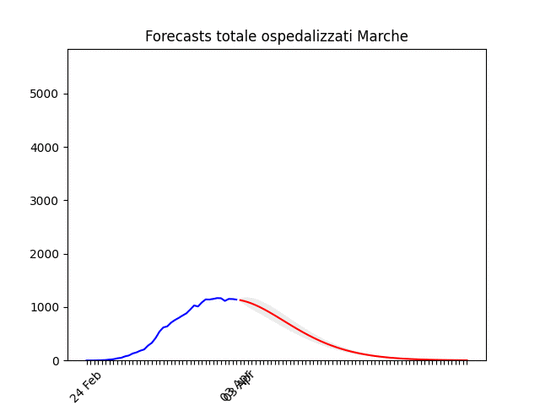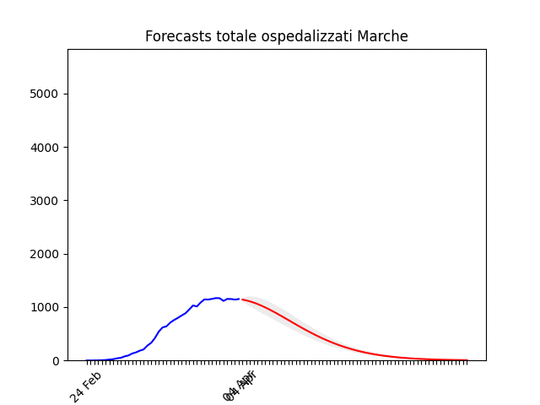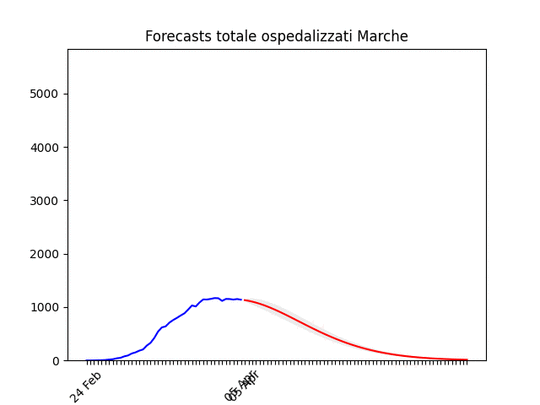Marche: Numero di ospedalizzati alla fine più alto del previsto (il 17 marzo ne avevamo previsto intorno a mille), ma si conferma oltre il picco.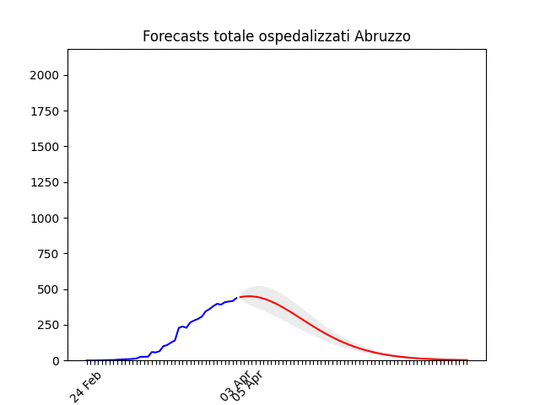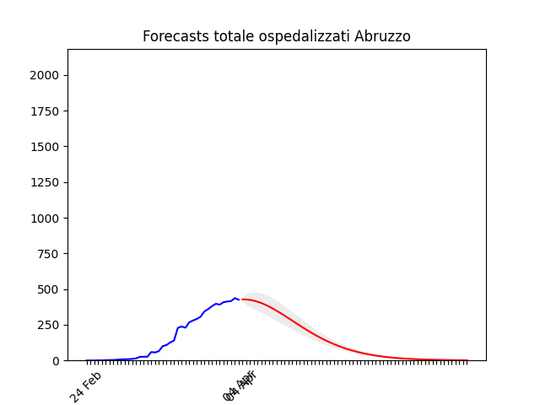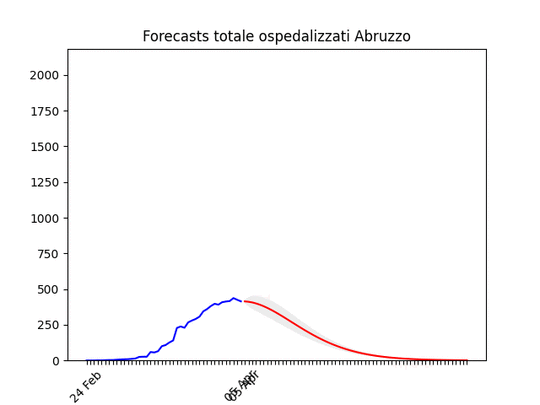Abruzzo: oltre il picco.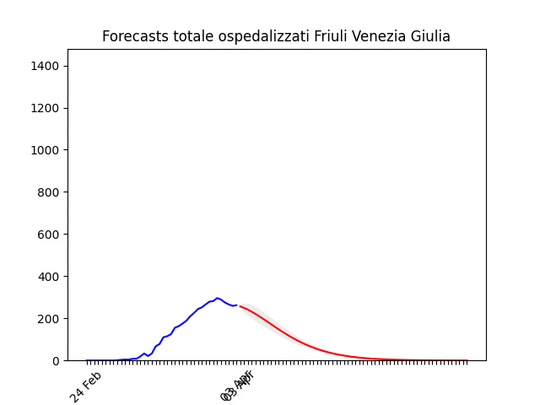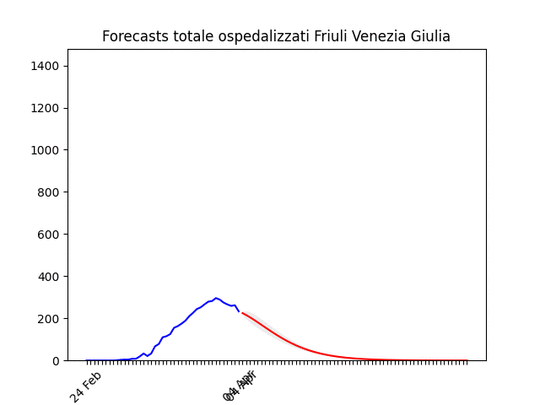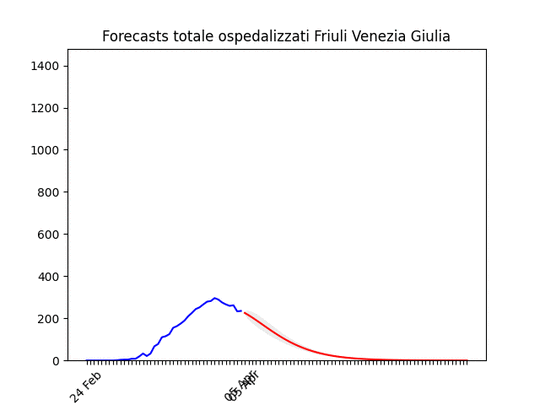Friuli Venezia-Giulia: scavallato da qualche giorno.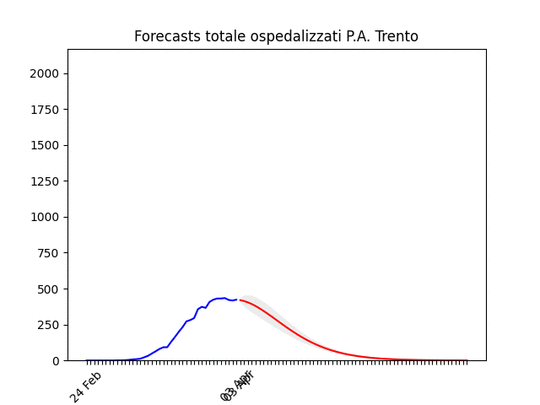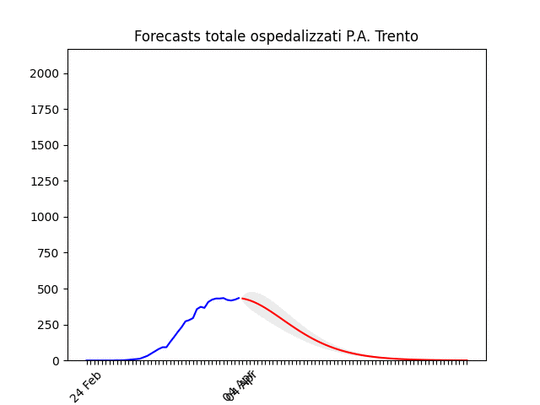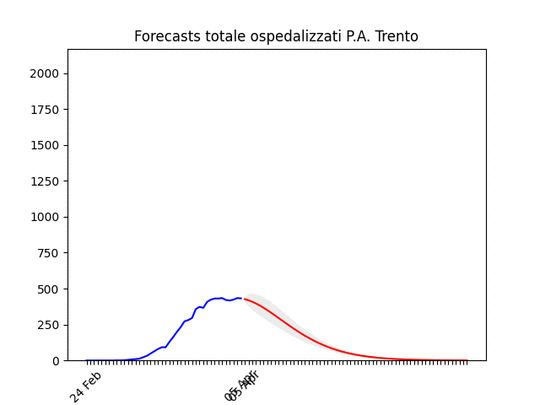Trento: “plateau”, ma dovrebbe iniziare a scendere presto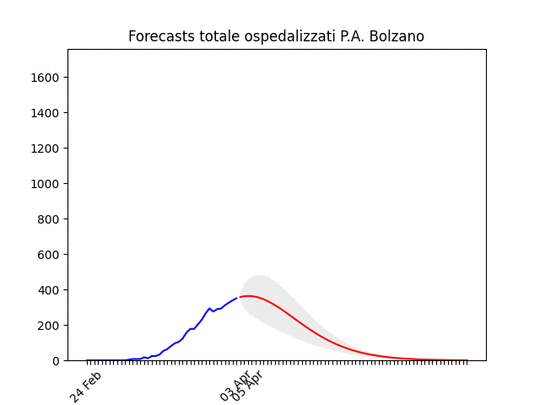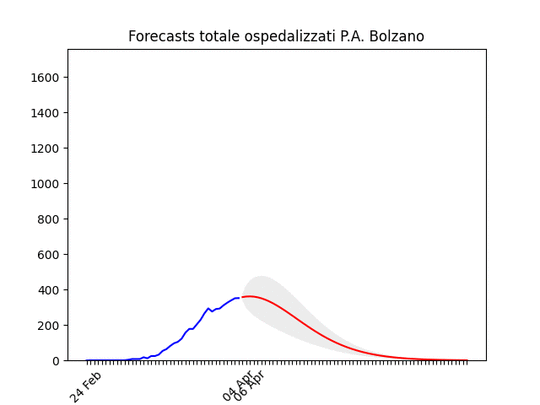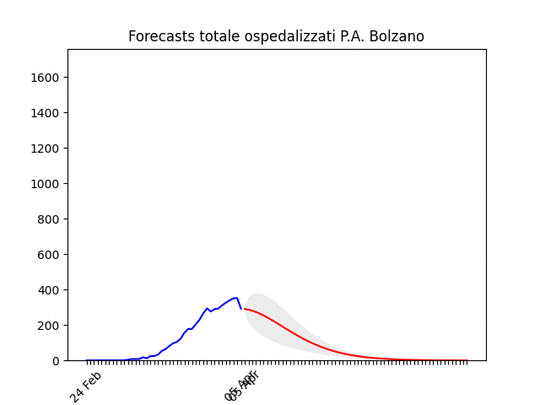Bolzano: caduta del numero di ospedalizzati ieri, probabilmente per un errore nella raccolta dati…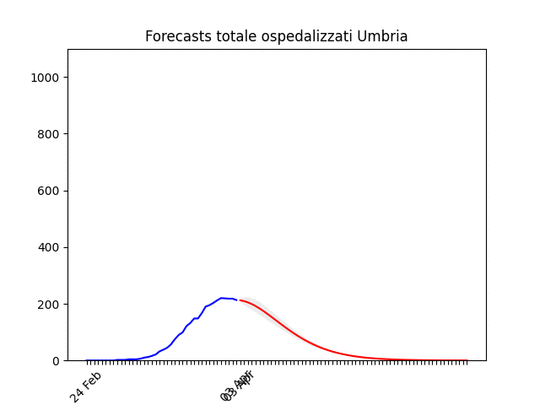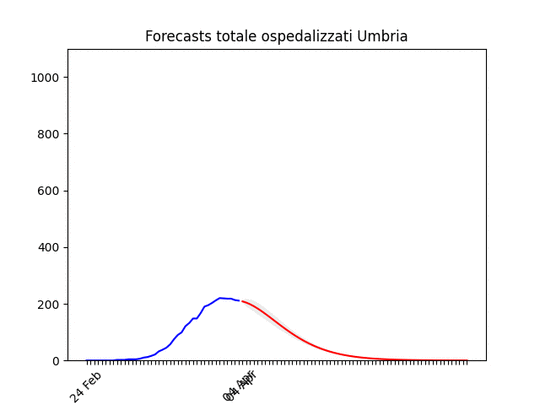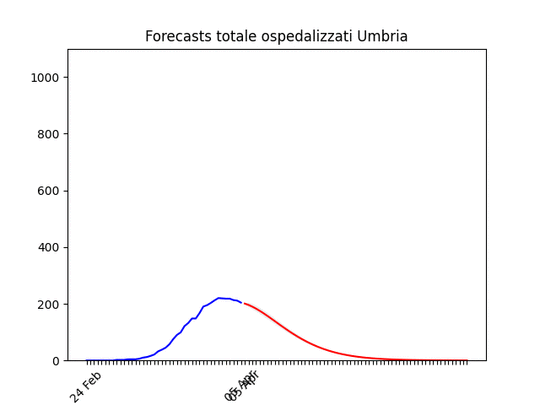Umbria: Oltre il picco.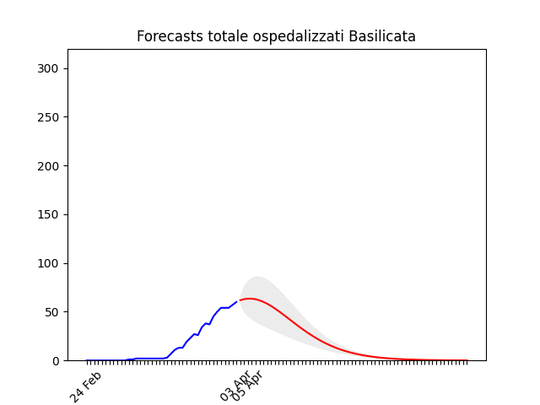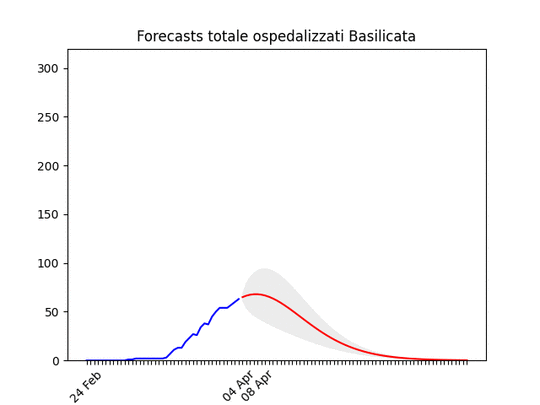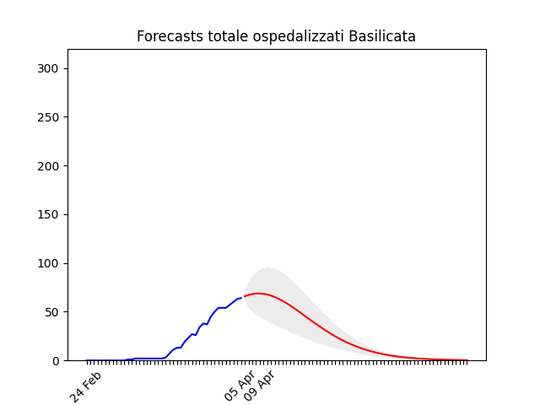Basilicata: si prevede ancora un piccolo aumento, ma il numero totale di ospedalizzati resta bassissimo.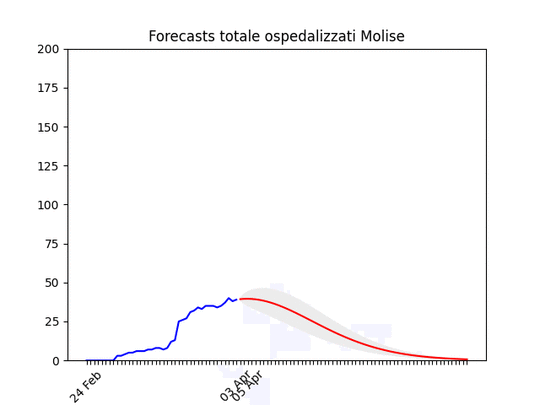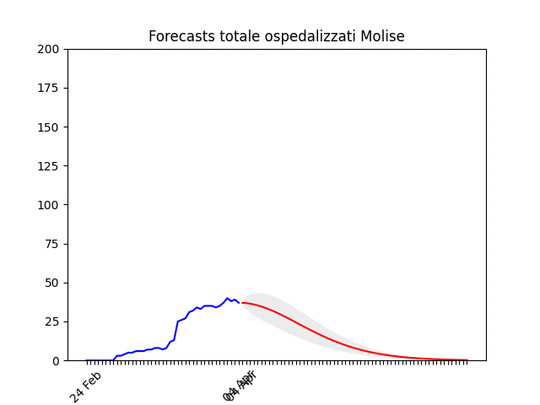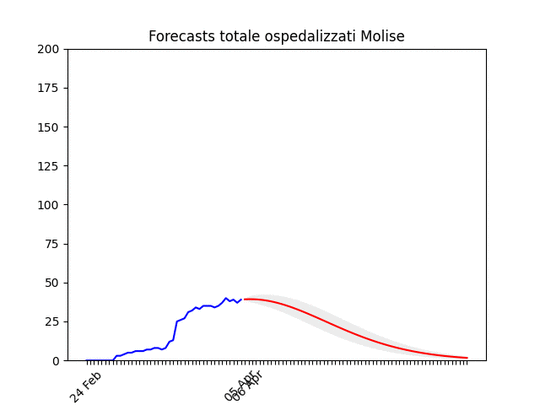Molise: pochissimi ospedalizzati.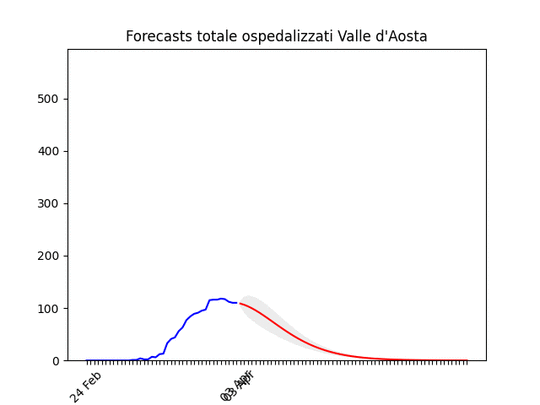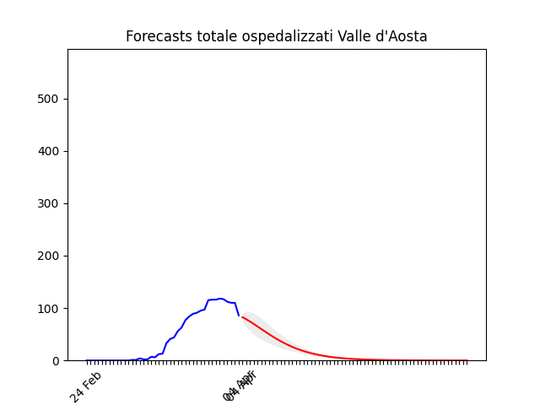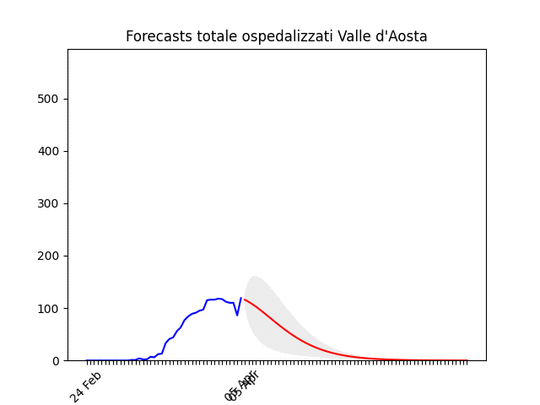Valle d’Aosta: Dati ballerini, ma anche qui in diminuzione.

Se già domenica 29 marzo, c’era stato un miglioramento in molte regioni, i dati di oggi 31 marzo lo confermano su tutta la linea. Non c’è bisogno di ulteriori commenti…

Modello usato. Dati protezione civile. Codice del programma.

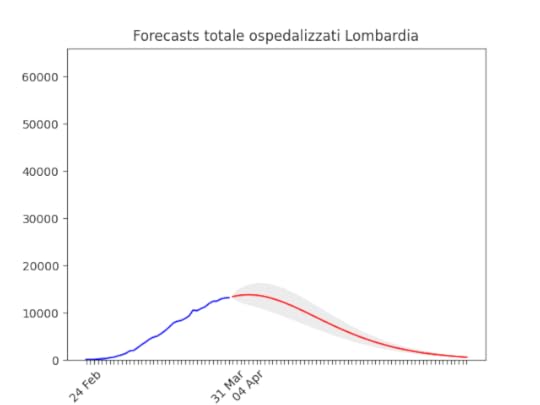Per fortuna le previsioni sembrano essere accurate, siamo decisamente vicino allo “scavallamento”.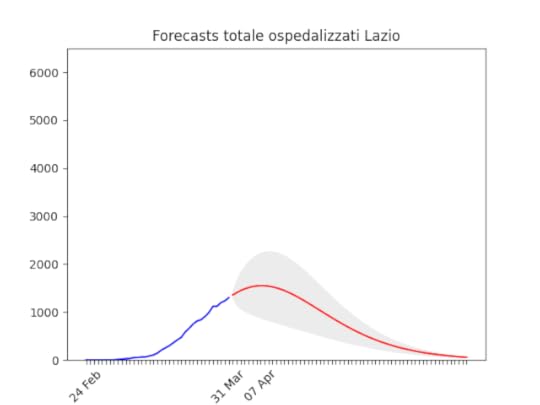Anche qui, si conferma il buon andamento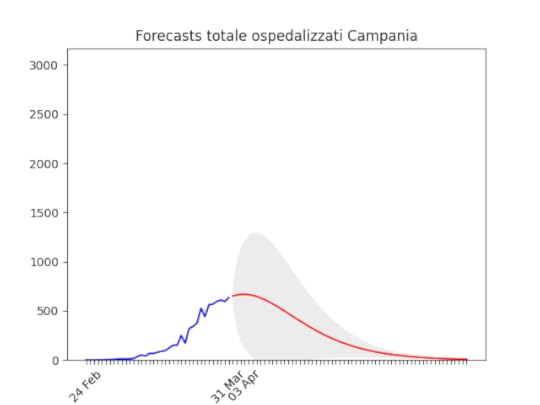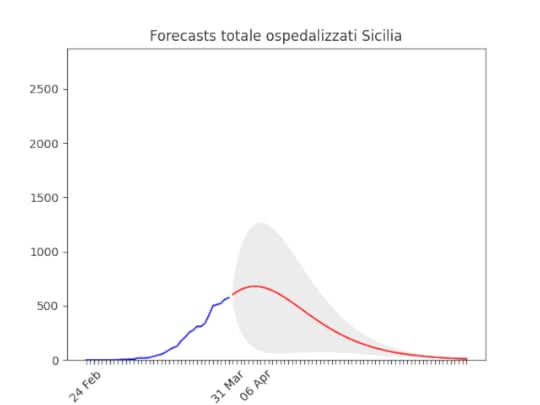Miglioramento anche qui.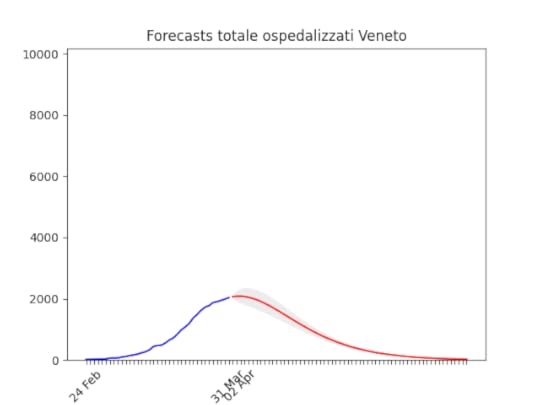Il miglioramento registrato domenica 29 si conferma.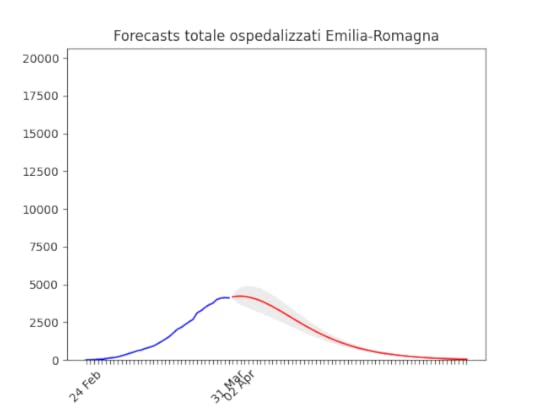Pur confermando un numero totale altissimo, anche qui la discesa si conferma.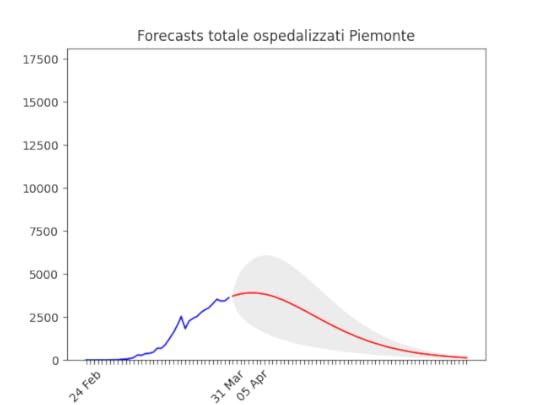Come scritto domenica 29, il picco si è allontanato (la “piccola discesa” era un errore nei dati), ma non di tanto.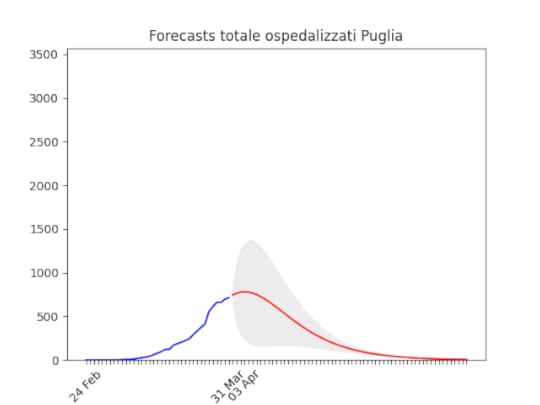Anche qui, si è confermata come prevista la flessione dei giorni antecedenti con conseguente miglioramento delle previsioni.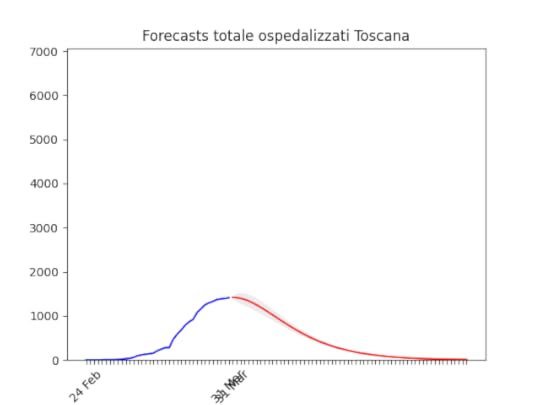Come per altre, praticamente scavallato.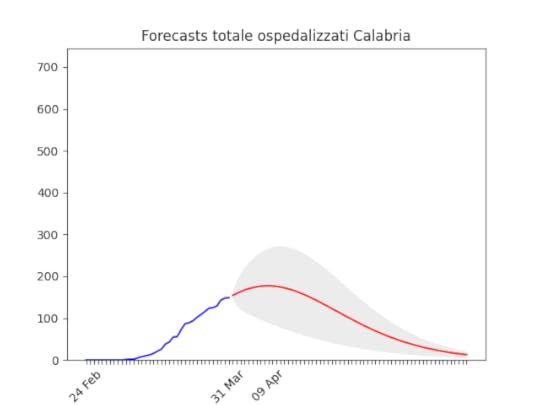Miglioramento anche qui, come confermato domenica.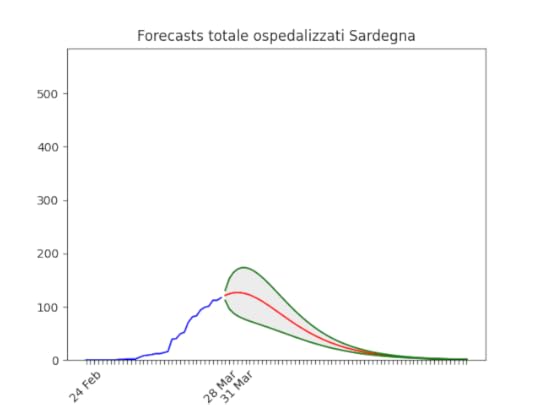L’andamento ondivago dei dati continua, e la nuova previsione non converge… lasciamo quella della settimana scorsa.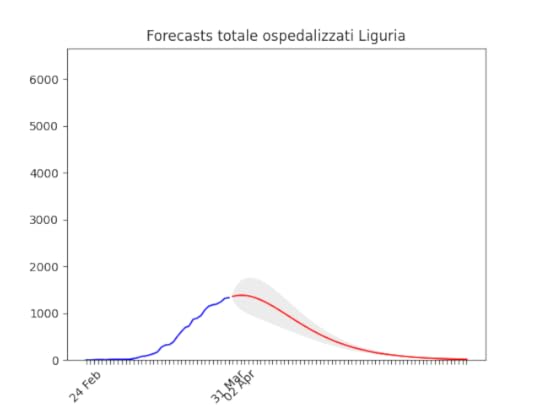Anche in Liguria miglioramento netto.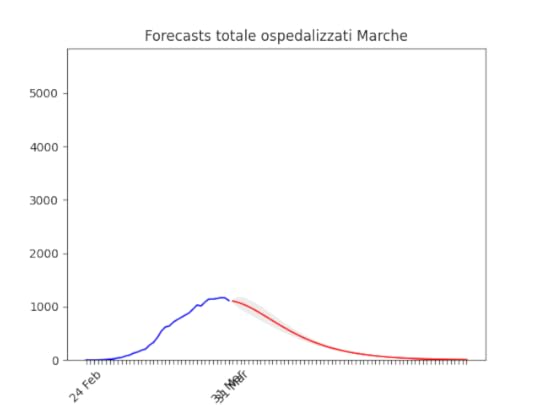Le Marche confermano di aver “scavallato”.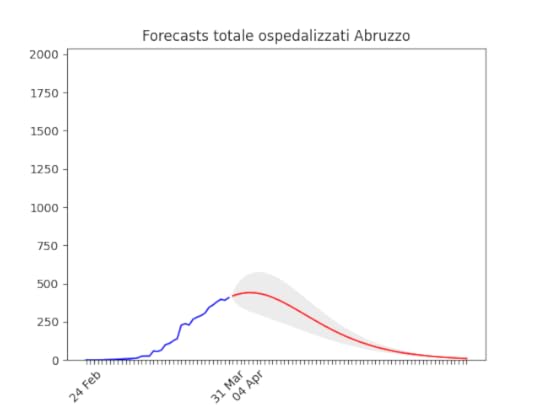Miglioramento anche qui.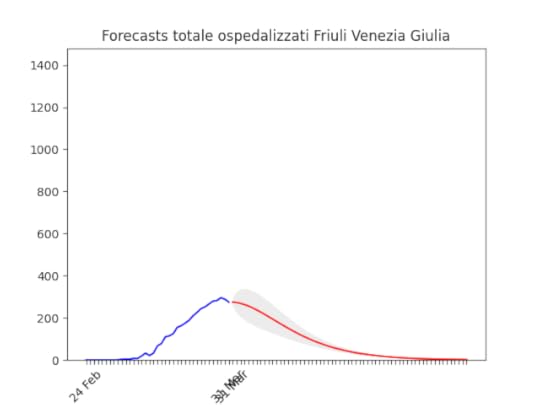Numero… in picchiata.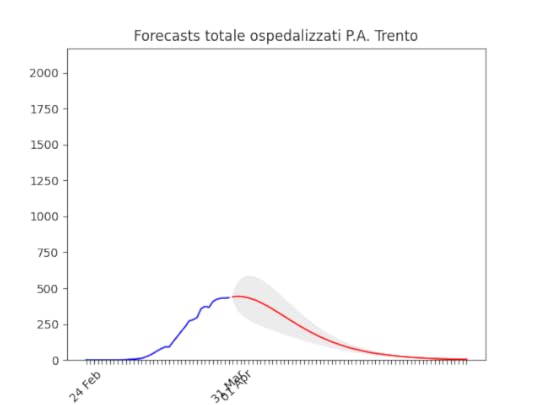Previsione ancora più rosea di domenica per Trento.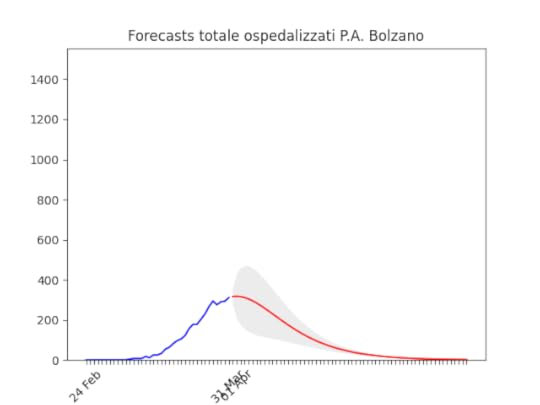Ci siamo anche qui…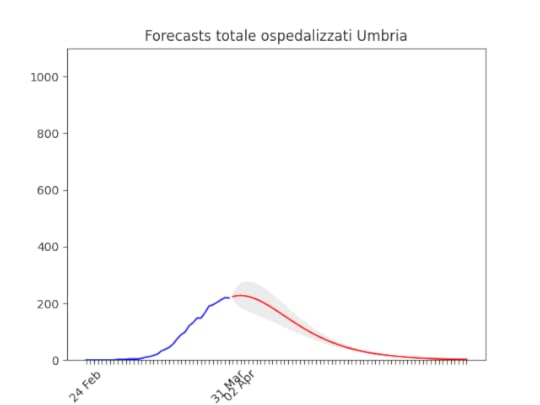Come sopra…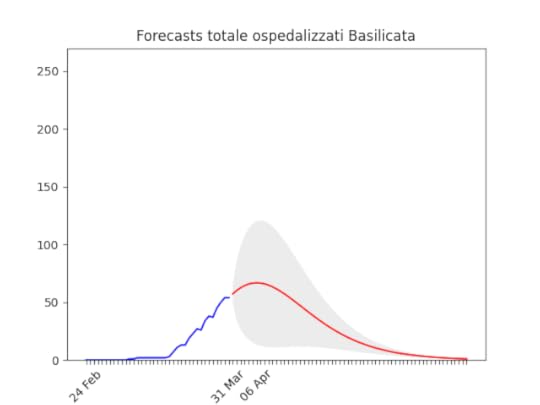Come sopra.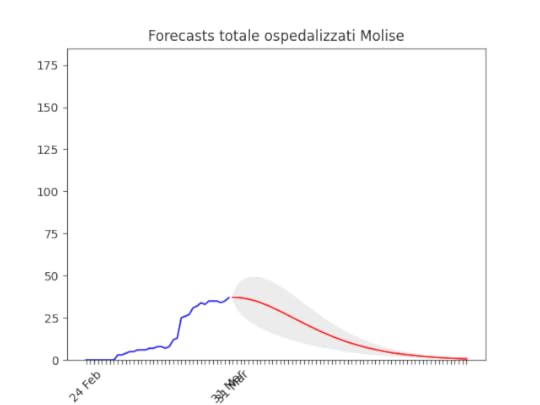Resta una delle regioni meno colpite.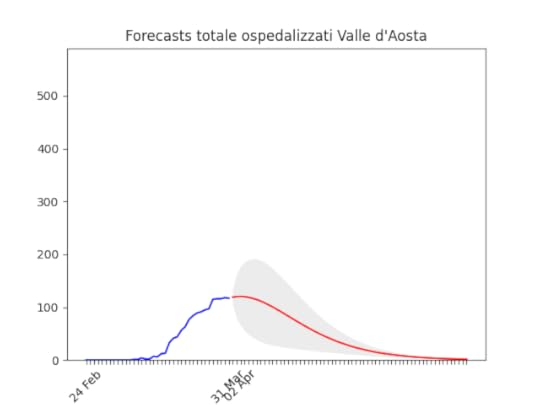Si conferma la conferma del miglioramento di domenica.

In this post I describe a Susceptible-Infectious-Recovered model and how I simplified it to fit actual data. The code for the fit is available on github, where you can find also forecasts for all countries. Data from Hopkins University.

Below the projections for a few countries, with comment:

Blue line: the dataRed line: best projectionGrey area: 70% confidence level (i.e. if it’s big the projection have high probability of being wrong)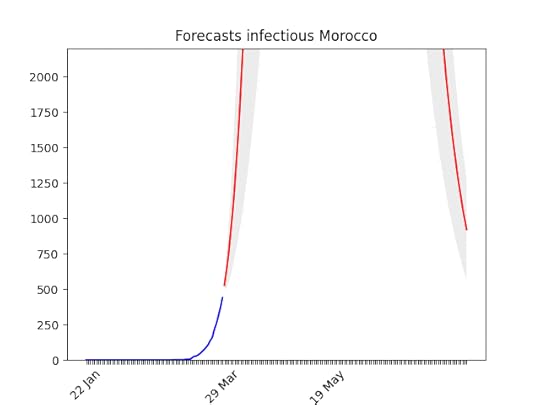

One known effect of the simplification I made is that forecasts for countries at the beginning of the epidemic are over-pessimistic. Have a look at Morocco for instance. With only 500 cases, and difficulties in imposing social restriction, it looks like the number of cases is going to skyrocket. Most probably, though, in a week the projection-curve will go down. In addition to that, the statistics (number of cases) at the beginning is, by definition, low, which means bad forecasts.

Actual Forecasts

Italy — static and animated forecasts.

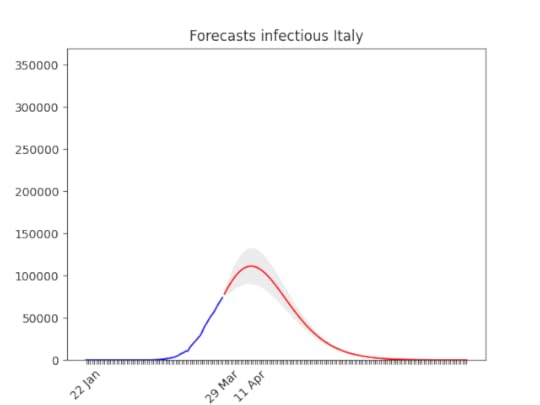Italy, march, 29: The confidence band (the grey area) is quite narrow now. See below the animation to see how the forecasts have improved with time, and why. The worst has yet to come, but it’s not far. In addition to that, a few regions are very close to the peak, others not so close–but the latter ones have less cases (see Italian regions forecasts).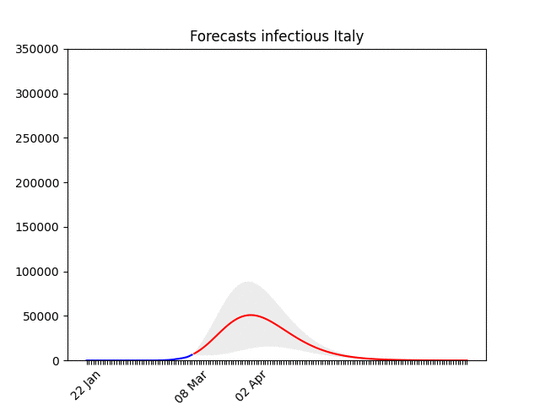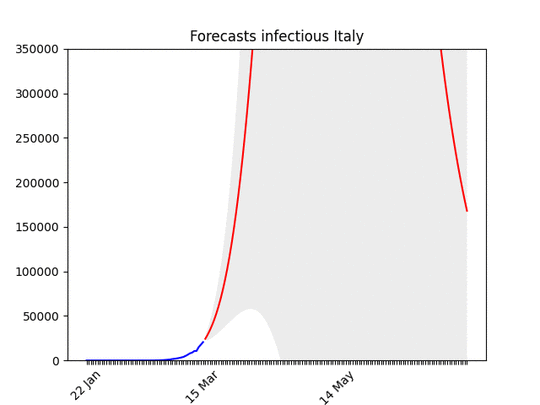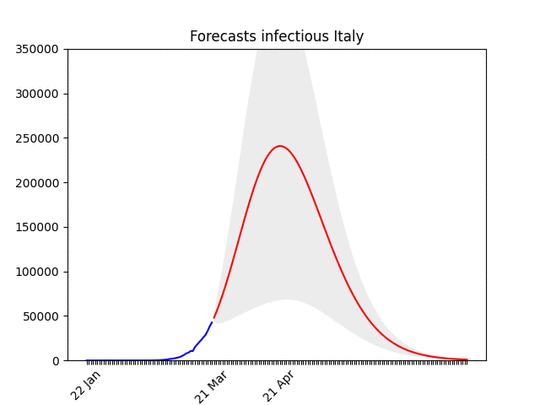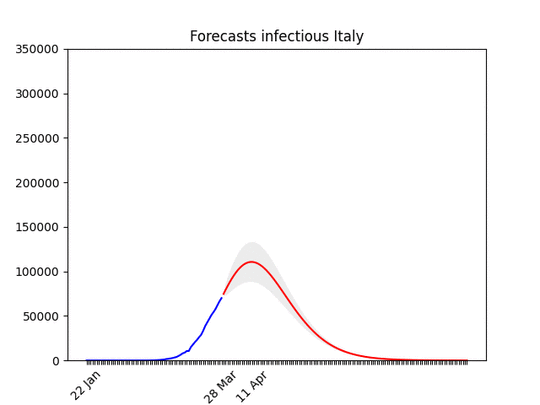Forecasts for Italy with latest data, and animation with all the forecasts made during the last 3 weeks: you can see how the forecasts improve with time. WIth the restriction it has gone down. This means that at the beginning, without social restriction, most probably the number would have grown considerably.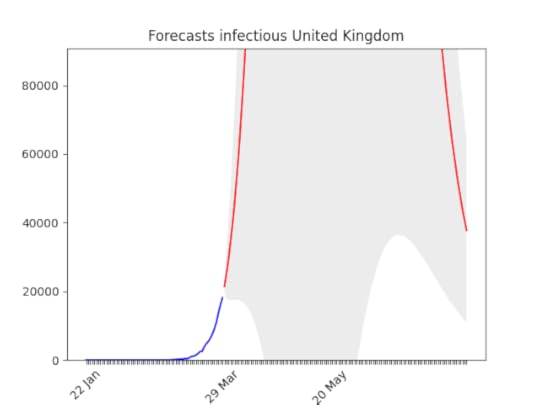Hard to believe, but the situation is actually improving (still, it looks not good). Remember that at the beginning of the epidemic, also Italy the number of infected people seemed to grow exponentially. With time it went down.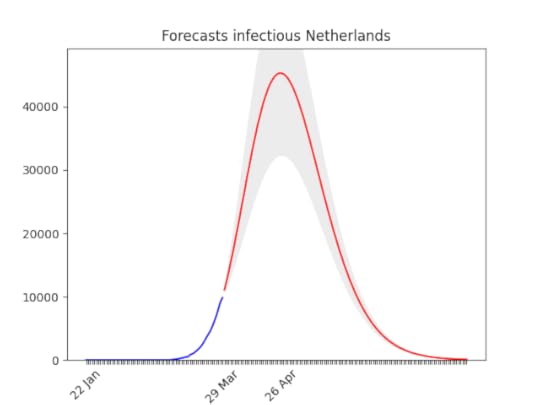In the Netherlands, the situation is improving by the day.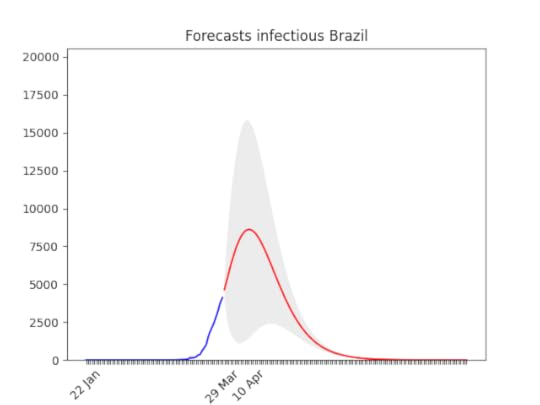Huge errors in the prediction. But you can see also by naked eye that data showed an improvement (apparently no one is listening the Brazilian president, and most people avoid social contact anyway).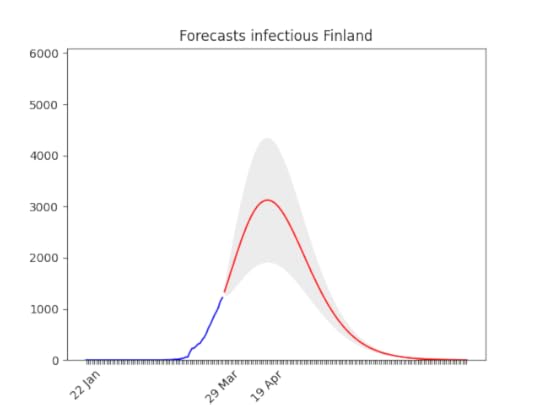After a bumpy start, the data show a clear direction. There might be changes in the next days, but most probably the peak will arrive in the second half of April, with a three-fold increase of cases.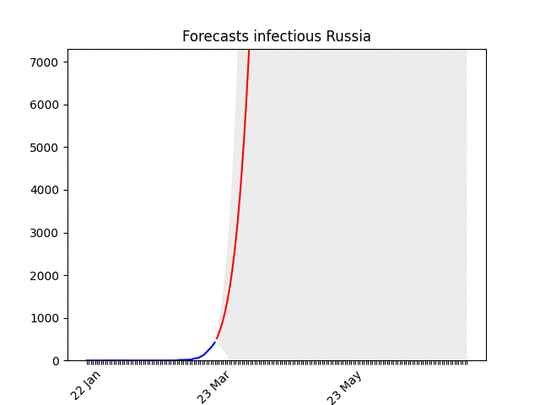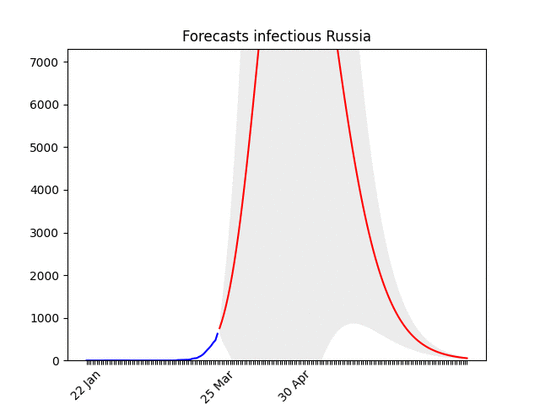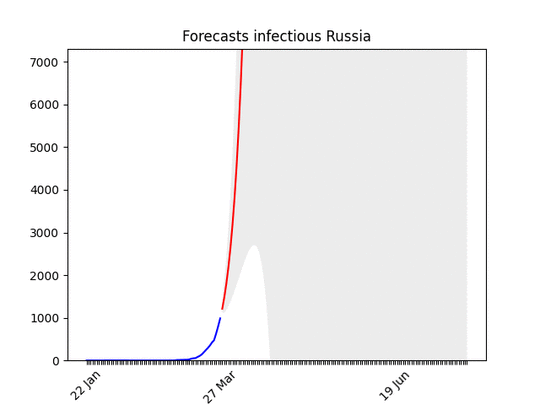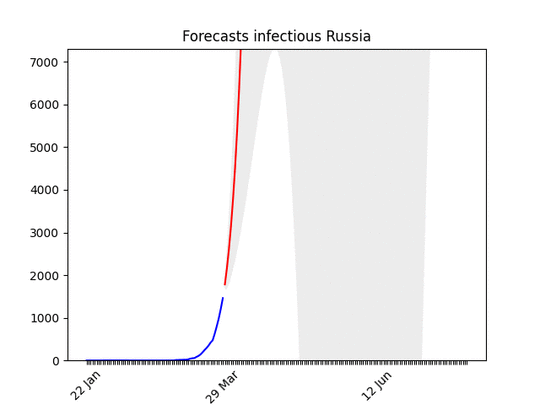I put the animation here, because the forecasts are not getting much better . They have improved only the last day, let’s hope this trend will continue then.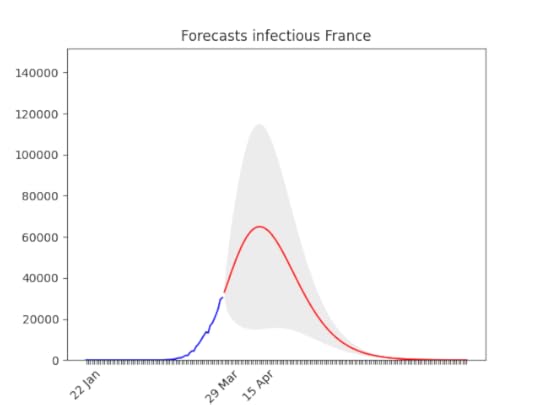Still big error (grey area), but the peak is forecasted here as well for the second half of April. The number of cases is going to be huge though, as Germany (see below).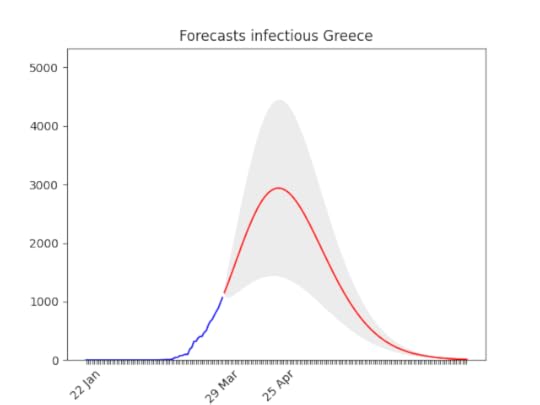As above, probably a bit later.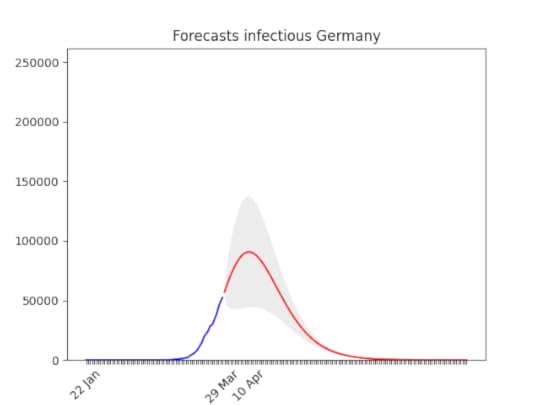It has grown super fast lately. It is worrying that it might arrive to a 150,000 cases –more than Italy.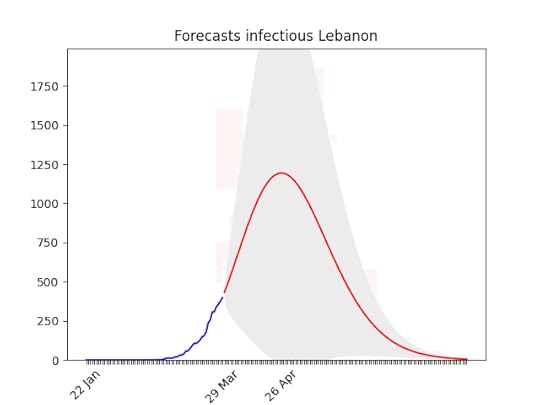huuuuge uncertainty on the forecasts (look at the data!), but there seems to be room for hope.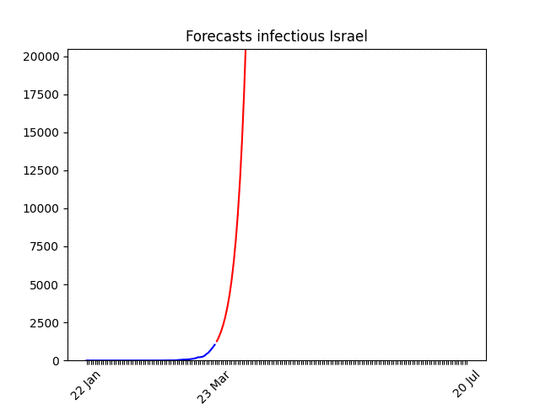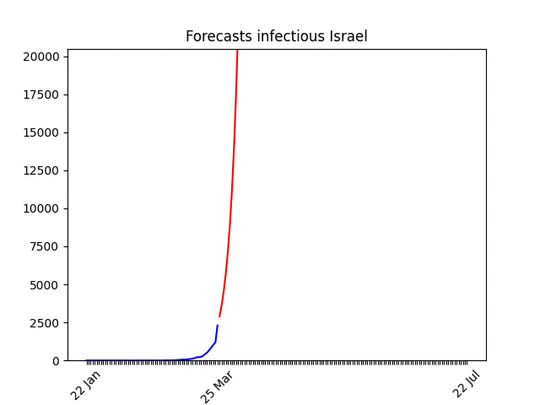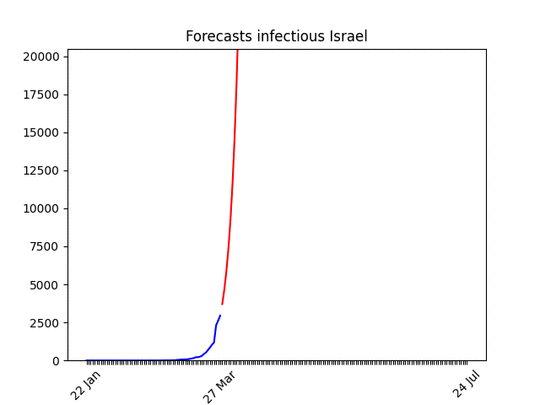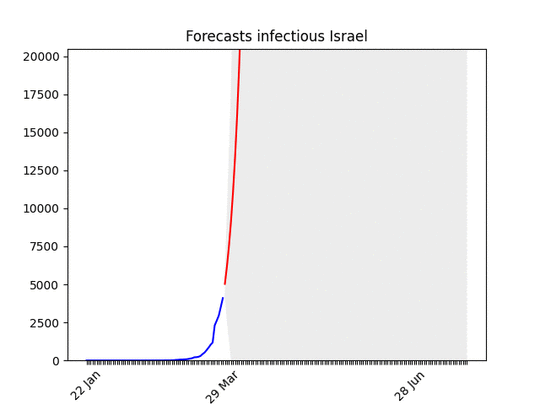I put the animation here just to show that the situation is improving. Most probably in a few days the shape of the forecasts will be similar to other countries.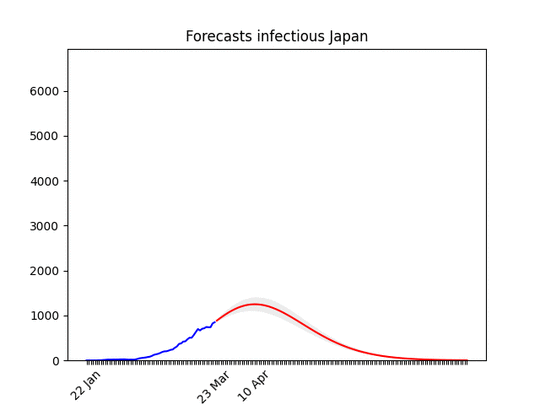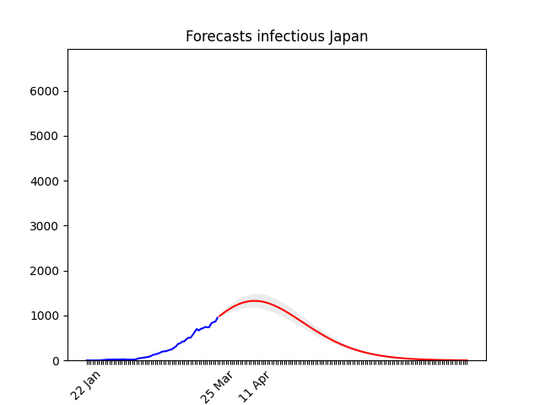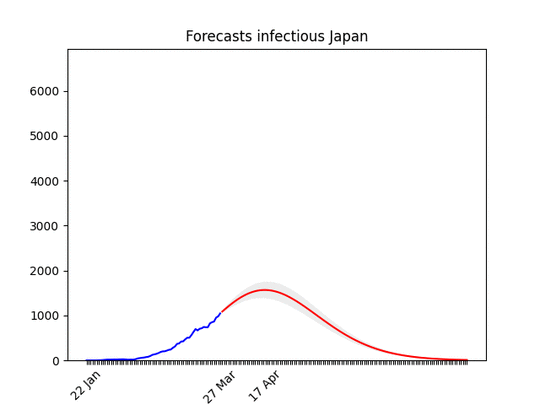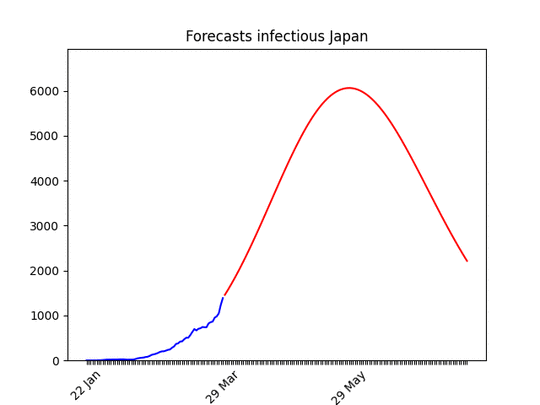Data in Japan show a big increase in the rate. Only for Japan, I took data from the past 21 days for the fit (instead of 14) and increased the smoothing process. I did that because I’m confident that the increase of the past days is temporary .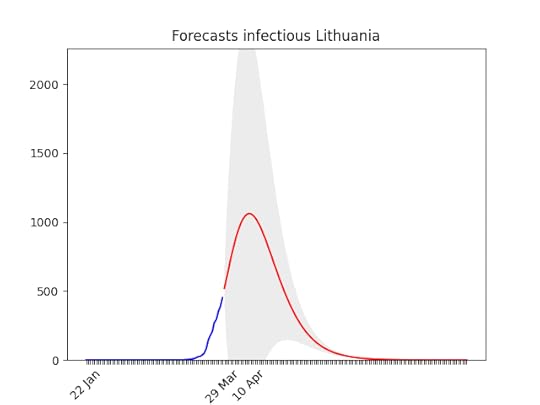Lithuania.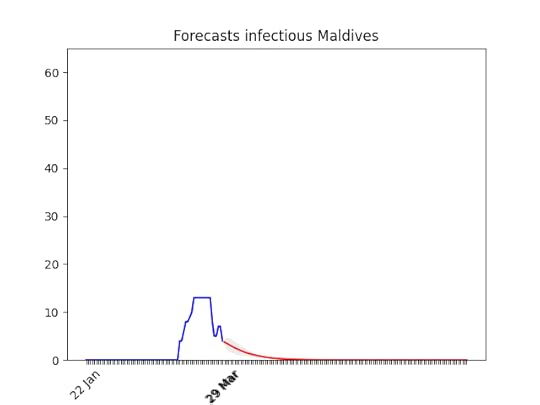Not bad… let’s see if the data were actually meaningful!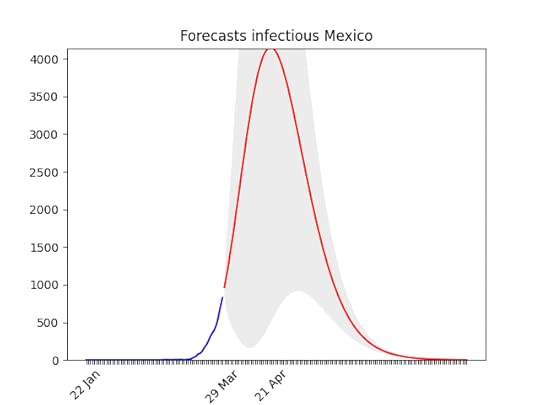The behaviour looks similar to the US, but without a huge number of cases.