Rob Pike's Blog

Towards the end of 2014, in need of pleasant distraction, I began writing, in Go, my second pseudo-APL, called Ivy. Over the years, Ivy's capabilities expanded to the point that it's now being used to do things such as to design floating-point printing algorithms. That was unexpected, doubly so because among the set of array languages founded by APL, Ivy remains one of the weakest.
Also unexpected was how the arrival of high-precision floating point in Go's libraries presented me with some mathematical challenges. Computing functions such as sine and cosine when there are more bits than the standard algorithms provide required polishing up some mathematics that had rusted over in my brain. In this article, I'll show the results and the sometimes surprising paths that led to them.
First I need to talk a bit more about Ivy itself.
For obvious reasons, Ivy avoids APL's idiosyncratic character set and uses ASCII tokens and words, just as in my previous, Lisp-written pseudo-APL back in 1979. To give it a different flavor and create a weak but valid justification for it, from the start Ivy used exact arithmetic, colloquially big ints and exact rationals. This made it unusual and a little bit interesting, and also meant it could be used to perform calculations that were clumsy or infeasible in traditional languages, particularly cryptographic work. The factorial of 100, in Ivy (input is indented):

  !100      93326215443944152681699238856266700490715968264381621468592963895217599993229915608941463976156518286253697920827223758251185210916864000000000000000000000000

Or perhaps more surprising:

    0.51/2

Ivy also became, due to the work of Hana Kim and David Crawshaw, the first mobile application written in Go. I take no credit for that. The iOS version is long gone and the Android version is very old, but that situation might change before long.
For those who don't know the history and peculiarities of APL, it's worth doing your own research; that education is not the purpose of this article. But to make the examples comprehensible to those sadly unfamiliar with it, there are a few details of its model one should understand to make sense of the Ivy examples below.
First, every operator, whether built-in or user-programmed, takes either one argument or two. If one, the operator precedes the argument; if two, the arguments are left and right of the operator. In APL, these are called monadic and dyadic operators. Because Ivy was written based on my fading memory of APL, rather than references, in Ivy they are called unary and binary. Some operators work in either mode according to the surrounding expression; consider

    1 - 2  # Binary: subtraction-1    - 0.5  # Unary: negation-1/2

The second detail is that values can be scalars or they can be multidimensional vectors or matrices. And the operators handle these in a way that feels deeply natural, which is part of why APL happened:

    4 5 6 - 22 3 4
    4 5 6 - 1 2 33 3 3

Compare those expressions to the equivalent in almost any other style of language to see why APL has its fans.
Finally, because the structure of APL expressions is so simple with only two syntactic forms of operators (unary and binary), operator precedence simply does not exist. Instead, expressions are evaluated from right to left, always (modulo parentheses). Thus
3 * 4 5
evaluates to 27 because it groups as 3 * (4 5): every operand is maximal length, traveling left, until an operator arrives. In most languages, the usual precedence rules would instead group this as (3*4) 5.
Enough preamble.
Ivy was fun to write, which was its real purpose, and there were some technical challenges, in particular how to handle the fluid typing, with things changing from integers to fractions, scalars to vectors, vectors to matrices, and so on. I gave a talk about this problem very early in Ivy's development, if you are interested. A lot has changed since then but the fundamental ideas persist.
Before long, it bothered me that I couldn't calculate square roots because Ivy did not handle irrational numbers, only exact integers and rationals. But Robert Griesemer, who had written the math/big library that Ivy used, decided to tackle high-precision floating point. This was important not just for Ivy, but for Go itself. The rules for constants in Go require that they can be represented to high precision in the source code, much more so than the usual 64-bit variables we are used to. That property allowed constant expressions involving floating-point numbers to be evaluated at compile time without losing precision.
At the time, the Go toolchain was being converted from the original C implementation to Go, and the constant evaluation code in the original compiler had some problems. Robert decided, with his usual wisdom and tenacity, to build a strong high-precision floating-point library that the new compiler could use. And Ivy would benefit.
By mid-2015, Ivy supported floats with lots of bits. Happiness ensued:

sqrt 21.41421356237 )format '%.50f' sqrt 21.41421356237309504880168872420969807856967187537695

Time to build in some helpful constants:

pi3.14159265358979323846264338327950288419716939937511 e2.71828182845904523536028747135266249775724709369996

Internally these constants are stored with 3000 digits and are converted on the fly to the appropriate precision, which is 256 bits by default but can be set much bigger:

)prec 10000       # Set the mantissa size in bits )format '%.300f'  # Set the format for printing values pi3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930381964428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141274

Now things get harder.
Square root is easy to calculate to arbitrary precision. Newton's method converges very quickly and we can even use a trick to speed it up: create the initial value by halving the exponent of the floating-point argument.
But what about sine, cosine, exponential, logarithm? These transcendental functions are problematic computationally. Arctangent is a nightmare.
When I looked around for algorithms to compute these functions, it was easy to find clever ways to compute accurate values with 64-bit floating-point (float64) inputs, but that was it. I had to get creative.
What follows is how I took on programming high-precision transcendental functions and their relatives. It was a lot of fun and I uncovered some fascinating things along the way.
Disclaimer: Before going further, I must admit that I am not an expert in numerical computation. I am not an expert in analysis. I am not an expert in calculus. I have just enough knowledge to be dangerous. In the story that follows, if I say something that's clearly wrong, I apologize in advance. If you see a way I could have done better, please let me know. I'd love to lift the game. I know for a fact that my implementations are imperfect and can get ratty in the last few bits. And I cannot state anything definitive about their error characteristics. But they were fun to puzzle out and implement.
In short, here follows the ramblings of a confessed amateur traversing unfamiliar ground.
The easiest transcendental functions to provide are sine, cosine, and exponential. These three are in fact closely related, and can all be computed well using their Taylor series, which converge quickly even for large values. Here for instance is the Taylor series (actually a Maclaurin series, since we start at 0) for exponential (thanks to Wikipedia—which, by the way, I support financially and hope you do too—for the screen grab of these equations):

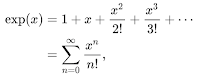
Those factorials in the denominator make this an effective way to compute the exponential. And the sine and cosine series are closely related, taking alternate (sine odd, cosine even) terms from the exponential, with alternating signs:


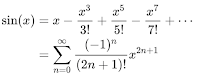
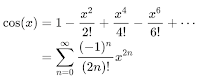
Euler's famous identity 

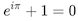
might help explain why these three functions are related. (Or not, depending on your sensibilities.)
The challenge with sine and cosine is not the calculation itself, but the process of argument reduction. Because these functions are periodic, and because small values of the argument do better in a Taylor series, it is a good idea to "reduce" or unwind the argument into the range of 0 to 2𝛑. For very large values, this reduction is hard to do precisely, and I suspect my simplistic code isn't great.
For tangent, rather than fight the much clumsier Taylor series, I just computed sin(x) and cos(x) and returned their quotient, with care.
That process of taking existing implementations and using identities to build a new function was central to how Ivy eventually supported complex arguments to these functions as well as hyperbolic variants of them all. For example, for complex tangent, we can use this identity:
tan(x yi) = (sin(2x) i sinh(2y))/(cos(2x) cosh(2y))
Here sinh is the hyperbolic sine, which is easy to compute given the exponential function or by just taking the odd terms of the Taylor series for exponential, while cosh takes the even terms. See the pattern?
Next up we have the inverse functions arcsine (asin) and arccosine (acos). They aren't too bad but their Taylor series have poor convergence when the argument is near ±1. So we grub around for helpful identities and come up with two:
asin(x) = atan(x/sqrt(1-x²)) acos(x) = π/2 - asin(x)
But that means we need arctangent (atan), and its Taylor series has awful convergence for x near 1, whose result should be the entirely reasonable π/4 or 45 degrees. An experiment showed that using the Taylor series directly at 1.00001 took over a million iterations to converge to a good value. We need better.
I did some more exploration and in one of my old schoolbooks I found this identity:
atan(x) = atan(y) atan((x-y)/(1 xy))
In this identity, y is a free variable! That allows us to do better. We can choose y to have helpful properties. Now:
tan(π/8) = √2-1
or equivalently,
atan(√2-1) = π/8
so we can choose y to be √2-1, which gives us
atan(x) = π/8 atan((x-y)/(1 xy))   # With y = √2-1
so all we need to compute now is one arctangent, that of (x-y)/(1 xy). The only concern is when that expression nears one. So there are several steps.
First, atan(-x) is -atan(x), so we take care of the sign up front to give us a non-negative argument.
Next if |1-x|< 0.5, we can use the identity above by recurring to calculate atan((x-y)/(1 xy)) with y=√2-1. It converges well.
If x is less than 1 the standard series works well:
atan(x) = x - x³/3 x⁵/5 - x⁷/7 ...
For values above 1, we use this alternate series:
atan(x) = π/2 - 1/x 1/3x³ -1/5x⁵ 1/7x⁷ - ...
Figuring all that out was fun, and the algorithm is nice and fast. (Values troublesomely close to 1 are picked off by the identity above.)
So now we have all the arc-trig functions, and in turn we can do the arc-hyperbolics as well using various identities.
With trigonometry out of the way, it's time to face logarithms and arbitrary powers. As with arctangent, the Taylor series for logarithm has issues. And we need logarithms to calculate arbitrary powers: using Ivy's notation for power,
x ** y
is the same as
e ** y*log x
That's the exponential function, which we have implemented, but this necessary rewrite relies on the logarithm of x.
(If the power is an integer, of course, we can just use exact multiplication, with a pretty algorithm I can't resist showing:

# pow returns x**exp where exp is an integer. op x pow exp = z = 1 :while exp > 0 :if 1 == exp&1 z = z*x :end x = x*x exp = exp>>1 :end z
.5 pow 31/8

That loop is logarithmic (ha!) in multiplications. It is an exercise for the reader to see how it works. If the exponent is negative, we just invert the result.)
The Taylor series for log(x) isn't great but if we set x=1-y we can use this series:
log (1-y) = -y - y²/2 - y³/3 ...
It converges slowly, but it does converge. If x is big, the convergence is very slow but that's easy to address. Since log(1/x) is -log(x), and 1/x is small when x is large, for large x we take the inverse and recur.
There's more we can do to help. We are dealing with floating-point numbers, which have the form (for positive numbers):

mantissa * 2**exponent

and the mantissa is always a value in the close/open range [0,0.5), so its series will converge well. Thus we rewrite the calculation as:

log(mantissa * 2**exponent) = log(mantissa) log(2)*exponent

Now we have a good mantissa we can use in the series and a working exponential function. All that's missing is an accurate value for log(2).
When I was doing this work, I spent a long but unsuccessful time looking for a 3,000-digit accurate value for log(2). Eventually I decided to use Ivy itself, or at least the innards, to compute it. In fact I computed 10,000 digits to be sure, and was able to spot-check some of the digits using https://numberworld.org/digits/Log(2)/, which had sample sparse digits, so I was confident in the result.
The calculation itself was fun. I don't remember exactly how I did it, but looking at it now one way would be to compute
log(0.5) = -log 2
with the series above. With x=0.5, 1-x also equals 0.5 so
log(2) = -log (0.5) = -(-0.5 - 0.5²/2 - 0.5³/3...)
and that converges quickly. The computation didn't take long, even for 10,000 digits.
I then saved the result as a constant inside Ivy, and had all that was needed for x**y.
Finally, if we need the logarithm of a negative or complex number, that's easy given what we've already built:
log(x) = log(|x|) * phase(x)
To compute the phase, we use the arctangent calculation we worked out before.
And with that, Ivy had square roots, trigonometry, hyperbolic trigonometry, logarithms and powers, all for the whole complex plane. That was it for quite a while.
But come late 2025, I decided to fill one gap that was bothering me: The gamma function 𝚪(z), which is defined by the integral

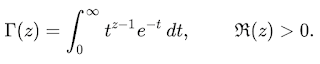
This function has many fascinating properties, but there are three that matter here. First is that if you play with that integral by parts you can discover that it has a recurrence relation
𝚪(z 1) = z𝚪(z)
which is a property shared by the factorial function:
z 1! = z!z
Because of this, the gamma function is considered one way to generalize factorial to non-integers, in fact to the whole complex plane except for non-positive integers, which are its poles. For real(z) < 0, we can (and do) use the identity
𝚪(z) = 𝛑/(sin(z𝛑)*𝚪(1-z))
It works out that for integer values,

𝚪(z 1) = z!

which means, if we so choose, we can define factorial over the complex plane using

z! = 𝚪(z 1)

APL and Ivy both do this.
The second property, besides being easy to evaluate for integer arguments because of the relation with factorial, is that it's also easy to evaluate at half-integers because
𝚪(½) = √π
and we can use the recurrence relation to get exact values for all positive half-integers (or at least, as exact as our value of π).
The third property is less felicitous: there is no easy way to compute 𝚪(z) for arbitrary z to high precision. Unlike the functions discussed above, there is no Taylor series or other trick, no known mechanism for computing the exact value for all arguments. The best we can do is an approximation, perhaps by interpolation between the values that we do know the exact value for.
With that dispiriting setup, we now begin our quest: How best to calculate 𝚪(z) in Ivy?
The first thing I tried was to use a method called the Lanczos approximation, which was described by Cornelius Lanczos in 1964. This gives a reasonable approximate value for 𝚪(z) for a standard floating-point argument. It gives 10-12 decimal digits of accuracy, and a float64 has about 16, float32 about 7. For Ivy we want to do better, but when I uncovered Lanczos's approximation it seemed a good place to start.
Here is the formula: 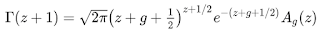with
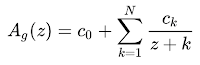Those c coefficients are the hard part: they are intricate to calculate. Moreover, because this is an approximation, not a series, we can't just compute a few terms and stop. We need to use all the terms of the approximation, which means deciding a priori how many terms to use. Plus, adding more terms does little to improve accuracy, so something like 10 terms is probably enough, given we're not going to be precise anyway. And as we'll see, the number of terms itself goes into the calculation of the c coefficients.
The Wikipedia page for the approximation is a good starting point for grasping all this. It has some sample coefficients and a Python implementation that's easy to relate to the explanation, but using it to calculate the coefficients isn't easy.
I found an article by Paul Godfrey very helpful (Lanczos Implementation of the Gamma Function). It turns the cryptic calculation in the Wikipedia article into a comprehensible burst of matrix algebra. Also, as a step along the way, he gives some sample coefficients for N=11. I used them to implement the approximation using Wikipedia's Python code as a guide, and it worked well. Or as well as it could.
However, if I were going to use those coefficients, it seemed dishonest not to calculate them myself, and Godfrey explains, if not exactly shows, how to do that.
He reduces the calculation of c coefficients to a multiplication of three matrices, D, B, C, and a vector F. I set about calculating them using Ivy itself. I do not claim to understand why the process works, but I am able to execute it.
D is straightforward. In fact its elements are found in my ex-Bell-Labs colleague Neil Sloane's Online Encyclopedia of Integer Sequences as number A002457. The terms are a(n) = (2n 1)!/n!², starting with n=1. Here's the Ivy code to do it (All of these calculations can be found in the Ivy GitHub repo in the file testdata/lanczos). We define the operator to calculate the nth element:

op A2457 n = (!1 2*n)/(!n)**2

The operator is called A2457 for obvious reasons, and it returns the nth element of the sequence. Then D is just a diagonal matrix of those terms, all but the first negated, which can be computed by

N = 6 # The matrix dimension, a small value for illustration here.
op diag v = d = count v d d rho flatten v @, d rho 0

The @ decorator iterates its operator, here a comma "raveling" or joining operator, over the elements of its left argument applied to the entire right. The diag operator then builds a vector by spreading out the elements of v with d zeros (d rho 0) between each, then reformats that into a d by d matrix (d d rho ...). That last expression is the return value: operators evaluate to the last expression executed in the body. Here's an example:

diag 1 2 3 4 5 61 0 0 0 0 00 2 0 0 0 00 0 3 0 0 00 0 0 4 0 00 0 0 0 5 00 0 0 0 0 6

For the real work, we pass a vector created by calling A2457 for each of 0 through 4 (-1 iota N-1), negating that, and adding an extra 1 at the beginning. Here's what we get:

D = diag 1, -A2457@ -1 iota N-1

D1    0    0    0    0    00   -1    0    0    0    00    0   -6    0    0    00    0    0  -30    0    00    0    0    0 -140    00    0    0    0    0 -630

B is created from a table of binomial coefficients. This turned out to be the most intricate of the matrices to compute, and I won't go through it all here, but briefly: I built Pascal's triangle, put an extra column on it, and rotated it. That built the coefficients. Then I took alternate rows and did a little sign fiddling. The result is an upper triangle matrix with alternating 1 and -1 down the diagonal.

B 1   1   1   1   1   1 0  -1   2  -3   4  -5 0   0   1  -4  10 -20 0   0   0  -1   6 -21 0   0   0   0   1  -8 0   0   0   0   0  -1

Again, if you want to see the calculation, which I'm sure could be done much more concisely, look in the repo.
Now the fun one. The third matrix, C, is built from the coefficients of successive Chebyshev polynomials of the first kind, called Tₙ(x). They are polynomials in x, but we only want the coefficients. That is, x doesn't matter for the value but its presence is necessary to build the polynomials. We can compute the polynomials using these recurrence relations:

T₀(x) = 1 T₁(x) = x Tₙ₊₁(x) = 2xTₙ(x) - Tₙ₋₁(x)
That's easy to code in Ivy. We treat a polynomial as just a vector of coefficients. Thus, as polynomials, 1 is represented as the vector
1
while x is
0 1
and x² is
0 0 1
and so on. To keep things simple, we always carry around a vector of all the coefficients, even if most are zero. In Ivy we can use the take operator to do this:

6 take 1

1 0 0 0 0 0

gives us a vector of length 6, with 1 as the first element. Similarly, we get the polynomial x by

6 take 0 10 1 0 0 0 0

The timesx operator shows why this approach is good. To multiply a polynomial by x, we just push it to the right and add a zero constant at the beginning. But first we should define the size of our polynomials, tsize, which needs to be twice as big as N because, as with the binomials, we will only keep alternate sets of coefficients.

tsize = -1 2*N
op timesx a = tsize take 0, a

That is, put a zero at the beginning of the argument vector and 'take' the first tsize elements of that to be returned.

timesx tsize take 0 1 # makes x²0 0 1 0 0 0 0 0 0 0 0

And of course to add two polynomials we just add the vectors.
Now we can define our operator T to create the Chebyshev polynomial coefficients.

op T n = n == 0: tsize take 1 n == 1: tsize take 0 1 (2 * (timesx T n-1)) - (T n-2) # Compare to the recurrence relation.

That T operator is typical Ivy code. The colon operator is a kind of switch/return: If the left operand is true, return the right operand. The code is concise and easy to understand, but can be slow if N is much bigger. (I ended up memoizing the implementation but that's not important here. Again, see the repo for details.) The rest is just recursion with the tools we have built.
To create the actual C matrix, we generate the coefficients and select alternate columns by doubling the argument to T. Finally, for reasons beyond my ken, the first element of the data is hand-patched to 1/2. And then we turn the vector of data into a square N by N matrix:

op gen x = (tsize rho 1 0) sel T 2*x
data =  flatten gen@ -1 iota tsize data[1] = 1/2
C=N N rho data
C1/2   0    0    0     0   0 -1   2    0    0     0   0  1  -8    8    0     0   0 -1  18  -48   32     0   0  1 -32  160 -256   128   0 -1  50 -400 1120 -1280 512

Phew. Now we just need F, and it's much easier. We need gamma for half-integers, which we know how to do, and then we can calculate some terms as shown in the article.

op gammaHalf n = # n is guaranteed here to be an integer plus 1/2. n = n - 0.5 (sqrt pi) * (!2*n) / (!n)*4**n
op fn z = ((sqrt 2) / pi) * (gammaHalf(z .5)) * (**(z g .5)) * (z g 0.5)**-(z 0.5)
F = N 1 rho  fn@ -1 iota N  # N 1 rho ... makes a vertical vector
F33.85781854717.568079439353.695149939672.341183884281.690936537321.31989578103

This code will seem like arcana to someone unaccustomed to array languages like APL and Ivy, but Ivy was actually a great tool for this calculation. To be honest, I started to write all this in Go but never finished because it was too cumbersome. The calculation of the C matrix alone took a page of code, plus some clever formatting. In Ivy it's just a few lines and is much more fun.
Now that we have all the pieces, we can do the matrix multiplication that Godfrey devised:
(D .*B .*C) .*F
Those are inner products: .* means multiply element-wise and then add them up (right to left, remember), standard matrix multiplication. We want the output to have high(ish) precision so print out lots of digits:

'%.22g' text (D .*B .*C) .*F

0.9999999981828222336458-24.7158058035104436273-19.21127815952716945532-2.463474009260883343571-0.0096359811628506495333873.228095448247356928485e-05

Using this method, I was able to calculate the coefficients exactly as they appear in Godfrey's article with size N=11. With these coefficients and the code modeled on the Python from Wikipedia, the result was 10 to 12 digits of gamma function.
I was thrilled at first, but the imprecision of the Lanczos approximation, for all its magic, nagged at me. Ivy is supposed to do better than 10 digits, but that's all we can pull out of Lanczos.
After a few days I went back to the web and found another approximation, one by John L. Spouge from 1994, three decades after Lanczos. It has the property that, although it's still only an approximation, the accuracy can be bounded and also tuned at the expense of more computation. That means more terms, but the terms are easy to calculate and the coefficients are much easier to calculate than with Lanczos, so much so that Ivy ends up computing them on demand. We just need a lot more of them.
Even better, I found a paper from 2021 by Matthew F. Causley that refined the approximation further to allow one to decide where the approximation can be most accurate. That paper is The Gamma Function via Interpolation by Matthew F. Causley, 2021.
Let's start with Spouge's original approximation, which looks like this:

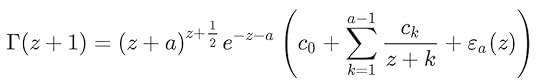
where

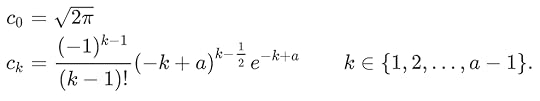
Notice that the variable a is not only the number of terms, it's also part of the calculations and the coefficients themselves. As in Lanczos, this is not a convergent series but an interpolated approximation. Once you decide on the value of a, you need to use all those terms. (I'll show you some of the coefficients later and you may be surprised at their value.)
The calculation may be long, but it's straightforward given all the groundwork we've laid in Ivy already and those c coefficients are easy to compute.
What Causley adds to this is to separate the number of terms, which he calls N, and the variable based on N that goes into the calculations themselves, which he calls r. In regular Spouge, a=r=N, but Causley splits them. Then, by brute force if necessary, we look for the value of r that gives us the best approximation at some value of z, called zbar, of our choosing. In Causley's paper, he shows his calculated N and optimal r values for a few integer values of zbar. The values in his table are not precise enough for our purposes, however. We need to compute our own.
Here it makes sense to calculate more terms than with Lanczos. Empirically I was able to get about half a digit for every term, and therefore decided to go with N=100, which gives about 50 digits or more, at least near zbar.
The calculation is much simpler than with Lanczos. Given N and r, here's how to calculate the vector of coefficients, cₙ:

op C n =

t = (1 -1)[n&1]/!n

u = e**r-n

v = (r-n)**n .5

t*u*v

c = N 1 rho (C@ iota N)

Once we have those coefficients, the gamma function itself is just the formula:

op gamma z =

p = (z r)**z-.5

q = **-(z r)

n = 0

sum = cinf

:while n <= N-1

sum = sum c[n]/(z n)

n = n 1

:end

p*q*sum

The variable cinf is straight from the paper. It appears to be a fixed value.

cinf = 2.5066 # Fixed by the algorithm; see Causley.

I ended up with N=100 and r=126.69 for zbar=6. Let's see how accurate we are.

)format %.70f # The number of digits for a 256-bit mantissa, not counting the 8 left of the decimal sign. gamma 1239916799.9999999999999999999999999999999999999999083377203094662100418136867266

The correct value is !11, which is of course an integer (and computed as such in Ivy):

!1139916800

They agree to 48 places, a huge step up from Lanczos and a difference unlikely to be noticed in normal work.
Have a gander at the first few of our cₙ coefficients with N=11 and r=126.69:

)format %.12e c 1.180698687310e 56-5.437816144514e 57 1.232332820715e 59-1.831910616577e 60 2.009185300215e 61-1.733868504749e 62 1.226116937711e 63...

They have many more digits than that, of course, but check out the exponents. We are working with numbers of enormous size; it's remarkable that they almost completely cancel out and give us our gamma function with such accuracy. This is indeed no Taylor series.
I chose N because I wanted good accuracy. I chose r because it gave me excellent accuracy at gamma 6 and thereabouts, well over 50 digits. To find my value of r, I just iterated, computing C and then gamma using values of r until the error between gamma 6 and !5 was as small as I could get. It's explained in the repo in the file testdata/gamma.
But there remains one mystery. In Causley's paper, r is closer to N, in fact always less than one away. So why did I end up with such a different value? The result I get with those parameters is excellent, so I am not complaining. I am just puzzled.
The optimization method is outlined in Causley's paper but not thorougly enough for me to recreate it, so I did something simpleminded: I just varied r until it gave good results at zbar=6. Perhaps that's naive. Or perhaps there is a difference in our arithmetical representation. Causley says he uses variable-precision arithmetic but does not quantify that. I used 256-bit mantissas. It's possible that the highest-precision part of the calculations is exquisitely sensitive to the size of the mantissa. I don't know, and would like to know, what's going on here. But there is no question that my values work well. Moreover, if I instead choose r=N, as in the original paper by Spouge, the answer has 38 good digits, which is less than in my version but also much more than a 64-bit float could deliver and perhaps more than Causley's technique could capture. (I do not mean to impugn Causley here! I just don't know exactly how he computed his values.)
However that may play out, there may be only one person who cares about the accuracy of the gamma function in Ivy. And that person thoroughly enjoyed exploring the topic and building a high-resolution, if necessarily imperfect, implementation.
Thanks for reading. If you want to try Ivy,
    go install robpike.io/ivy@latest

 

On BloatOn Bloat

The link below holds the slides from a talk I gave last year for the Commonwealth Bank of Australia's annual tech conference. They are mostly self-explanatory, with the possible exception of the "attractive nuisance" slide, for which I explained how a small package with good intentions can accumulate both a large set of dependents and a large set of dependencies, turning it into a vector for bloat and malfeasance.

Click here: On Bloat

 

This is my closing talk (video) from the GopherConAU conference in Sydney, given November 10, 2023, the 14th anniversary of Go being launched as an open source project. The text is interspersed with the slides used in the presentation.

What We Got Right, What We Got Wrong

INTRODUCTION

Hello.

Let me start by thanking Katie and Chewy for the giving me the honor of presenting the closing talk for the conference. And apologize for reading this from my script but I want to get the words right.

November 10, 2009

Today is November 10, 2023, the 14th anniversary of the launch of Go as an open source project.

That day, at 3pm California time if memory serves, Ken Thompson, Robert Griesemer, Russ Cox, Ian Taylor, Adam Langley, Jini Kim and I watched expectantly as the site went live and the world learned what we had been up to.

Fourteen years later, there is much to look back on. Today I'd like to take the opportunity to talk about some of the larger lessons learned since that day. Even the most successful projects have things that, upon reflection, could have been done better. And of course, things that in hindsight seem to have been key to their success.

Up front I must make clear that I am speaking only for myself, not for the Go team and not for Google.  Go was and still is a huge effort by a dedicated team and a huge community, so if you agree with anything I say, thank them. If you disagree, blame me but please keep it to yourself 😃.

Given the title of this talk, many people might expect I'm going to be analyzing good and bad things in the language. Of course I'll do some of that, but much more besides, for several reasons.

First, what's good and bad in a programming language is largely a matter of opinion rather than fact, despite the certainty with which many people argue about even the most trivial features of Go or any other language.

Also, there has already been plenty of discussion about things such as where the newlines go, how nil works, using upper case for export, garbage collection, error handling, and so on.  There are certainly things to say there, but little that hasn't already been said.

But the real reason I'm going to talk about more than the language is that that's not what the whole project was about. Our original goal was not to create a new programming language, it was to create a better way to write software. We had issues with the languages we were using—everyone does, whatever the language—but the fundamental problems we had were not central to the features of those languages, but rather to the process that had been created for using them to build software at Google.

The first gopher on a t-shirt

The creation of a new language provided a new path to explore other ideas, but it was only an enabler, not the real point. If it didn't take 45 minutes to build the binary I was working on at the time, Go would not have happened, but those 45 minutes were not because the compiler was slow, because it wasn't, or because the language it was written in was bad, because it wasn't. The slowness arose from other factors.

And those factors were what we wanted to address: The complexities of building modern server software: controlling dependencies, programming with large teams with changing personnel, ease of maintainability, efficient testing, effective use of multicore CPUs and networking, and so on.

In short, Go is not just a programming language. Of course it is a programming language, that's its definition, but its purpose was to help provide a better way to develop high-quality software, at least compared to our environment 14 plus years ago.

And that's still what it's about today. Go is a project to make building production software easier and more productive.

A few weeks back, when starting to prepare this talk, I had a title but little else.  To get me going, I asked people on Mastodon for input. A fair few responded, and I noticed a trend in the replies: people thought the things we got wrong were all in the language, but those we got right were in the larger story, the stuff around the language like gofmt and deployment and testing. I find that encouraging, actually. What we were trying to do seems to have had an effect.

But it's worth admitting that we didn't make clear early on what the true goals were. Perhaps we felt they were self-evident.  To address that shortcoming, in 2013 I gave a talk at the SPLASH conference entitled, Go at Google: Language Design in the Service of Software Engineering.

Go at Google

That talk and associated blog post are perhaps the best explanation of why Go happened.

Today's talk is something of a follow-on to the SPLASH talk, looking back on the lessons learned once we got past building the language and could apply ourselves to the bigger picture more broadly.

And so... some lessons.

First, of course, we have:

The Gopher

It may seem an odd place to start, but the Go gopher is one of the earliest factors in Go's success.  We knew long before the launch that we wanted a mascot to adorn the schwag - every project needs schwag - and Renee French offered to create one for us. We got that part absolutely right.

Here is a picture of the very first instance of the gopher plushie.

The gopher

And here is a picture of the gopher with the less successful first prototype.

The gopher with his less evolved ancestor

The Gopher is a mascot who serves as a badge of honor, even an identifier for Go programmers everywhere.  At this moment you are in a conference, one of many, called GopherCon.  Having a recognizable, funny creature ready to share the message from day one was vital to Go's growth.  Its goofy yet intelligent demeanor—he can build anything!

Gophers building a robot (drawing by Renee French)

—sets the tone for the community's engagement with the project, one of technical excellence allied with real fun. Most important, the gopher serves as a banner for the community, a flag to rally around, especially in the early days when Go was still an upstart in the programming world.

Here's a picture of gophers attending a conference in Paris some years back. Look how excited they are!

Gopher audience in Paris (photo by Brad Fitzpatrick)

All that said, releasing the Gopher design under a Creative Commons Attribution license was perhaps not the best choice.  On the one hand, it encouraged people to remix him in fun ways, which in turn helped foster community spirit.

Gopher model sheet

Renee created a "model sheet" to help artists work with him while keeping him true to his spirit.

Some artists had fun playing with these characteristics and making their own versions of him; Renee and my favorites are the ones by the Japanese designer @tottie:

@tottie's gophers

and game programmer @tenntenn:

@tenntenn's gopher

But the "attribution" part of the license often resulted in frustrating arguments, or in false credit given to Renee for creations that were not hers and not in the spirit of the original. And, to be honest, the attribution was often honored only reluctantly or not at all. For instance, I doubt @tenntenn was compensated or even acknowledged for this use of his gopher illustration.

gophervans.com: Boo!

So if we were doing it over, we'd think hard about the best way to make sure the mascot stays true to his ideals. It's a hard problem, maintaining a mascot, and the solution remains elusive.

But on to more technical things.

Done Right

Here is a list of things that I think we got objectively right, especially in retrospect.  Not every language project has done these things, but each was crucial to the ultimate success of Go. I'll try to be brief, because they will all be familiar topics.

1. Specification. We started with a formal specification. Not only does that lock down behavior when writing a compiler, it enables multiple implementations to coexist and agree on that behavior. A compiler alone is not a specification. What do you test the compiler against?

The specification, as seen on the web

Oh and by the way, the first draft of the specification was written here, on the 18th floor of a building on Darling Harbour in Sydney. We are celebrating Go's birthday in Go's home town.

2. Multiple implementations. There are multiple compilers, all implementing the same spec. Having a spec makes this much easier to achieve.

Ian Taylor surprised us when he sent mail one day informing us that, having read our draft spec, he'd written a compiler himself.

    Subject: A gcc frontend for Go

    From: Ian Lance Taylor

    Date: Sat, Jun 7, 2008 at 7:06 PM

    To: Robert Griesemer, Rob Pike, Ken Thompson

    One of my office-mates pointed me at http://.../go_lang.html .  It

    seems like an interesting language, and I threw together a gcc

    frontend for it.  It's missing a lot of features, of course, but it

    does compile the prime sieve code on the web page.

That was mind-blowing, but many more have followed, all made possible by the existence of a formal specification.

Lots of compilers

Having multiple compilers helped us refine the language and polish the specification, as well as providing an alternative environment for others less enamored with our Plan-9-like way of doing business.

(More about that later.)

Today there are lots of compatible implementations, and that's great.

3. Portability. We made cross-compilation trivial, which allowed

programmers to work on whatever platform they liked, and ship to whatever platform was required. This may be easier with Go than with any other language.  It's easy to think of the compiler as

native to the machine it runs on, but it has no reason to be.

Breaking that assumption is powerful and was news to many developers.

Portability

4. Compatibility. We worked hard to get the language in shape for

version 1.0, and then locked it down with a compatibility guarantee. Given what a dramatic, documented effect that made on Go's uptake, I find it puzzling that most other projects have resisted doing this.  Yes, there's a cost in maintaining strong compatibility, but it blocks feature- itis and, in a world in which almost nothing else is stable, it's delightful not to have to worry about new Go releases breaking your project.

The Go compatibility promise

5. The library. Although it grew somewhat as an accident, as there was no other place to install Go code at the beginning, the existence of a solid, well-made library with most of what one needed to write 21st century server code was a major asset. It kept the community all working with the same toolkit until we had experience enough to understand what else should be made available. This worked out really well and helped prevent variant libraries from arising, helping unify the community.

The library

6. Tools. We made sure the language was easy to parse, which enabled tool-building. At first we thought we'd need an IDE for Go, but easy tooling meant that, in time, the IDEs would come to Go. And along with gopls, they have, and they're awesome.

Tools

We also provided a set of ancillary tools with the compiler, such as automated testing, coverage, and code vetting. And of course the go command, which integrated the whole build process and is all many projects need to build and maintain their Go code.

Fast builds

Also, it didn't hurt that Go acquired a reputation for fast builds.

7. Gofmt. I pull gofmt out as a separate item from tools because it is the tool that made a mark not only on Go, but on the programming community at large. Before Robert wrote gofmt (which, by the way, he insisted on doing from the very beginning), automated formatters were not high quality and therefore mostly unused.

Gofmt proverb

Gofmt showed it could be done well, and today pretty much every language worth using has a standard formatter. The time saved by not arguing over spaces and newlines is worth all the time spent defining a standard format and writing this rather difficult piece of code to automate it.

Also, gofmt made countless other tools possible, such as simplifiers, analyzers and even the code coverage tool. Because gofmt's guts became a library anyone could use, you could parse a program, edit the AST, and just print byte-perfect output ready for humans to use as well as machines.

Thanks, Robert.

Enough with the congratulations, though. On to some more contentious topics.

Concurrency

Concurrency is contentious? Well, it certainly was in 2002, the year I joined Google. John Ousterhout had famously written that threads were bad, and many people agreed with him because they seemed to be very hard to use.

John Ousterhout doesn't like threads

Google software avoided them almost always, pretty much banning them outright, and the engineers doing the banning cited Ousterhout. This bothered me. I'd been doing concurrency-like things, sometimes without even realizing it, since the 1970s and it seemed powerful to me. But upon reflection it became clear that Ousterhout was making two mistakes. First, he was generalizing beyond the domain he was interested in using threads for, and second, he was mostly complaining about using them through with clumsy low-level packages like pthread, and not about the fundamental idea.

It's a mistake common to engineers everywhere to confuse the solution and the problem like this. Sometimes the proposed solution is harder than the problem it addresses, and it can be hard to see there is an easier path. But I digress.

I knew from experience that there were nicer ways to use threads, or whatever we choose to call them, and even gave a pre-Go talk about them.

Concurrency in Newsqueak

But I wasn't alone in knowing this; a number of other languages, papers, and even books had been written about concurrent programming that showed it could be done well. It just hadn't caught on as a mainstream idea yet, and Go was born partly to address that. In that legendary 45-minute build I was trying to add a thread to a non-threaded binary, and it was frustratingly hard because we were using the wrong tools.

Looking back, I think it's fair to say that Go had a significant role in convincing the programming world that concurrency was a powerful tool, especially in the multicore networked world, and that it could be done better than with pthreads. Nowadays most mainstream languages have good support for concurrency.

Google 3.0

Also, Go's version of concurrency was somewhat novel, at least in the line of languages that led to it, by making goroutines unflavored.  No coroutines, no tasks, no threads, no names, just goroutines. We invented the word "goroutine" because no existing term fit. And to this day I wish the Unix spell command would learn it.

As an aside, because I am often asked about it, let me speak for a minute about async/await.  It saddens me a bit that the async/await model with its associated style is the way many languages have chosen to support concurrency, but it is definitely a huge improvement over pthreads.

Compared to goroutines, channels, and select, async/await is easier and smaller for language implementers to build or to retrofit into existing platforms. But it pushes some of the complexity back on the programmer, often resulting in what Bob Nystrom has famously called "colored functions".

What Color is Your Function?

I think Go shows that CSP, which is a different but older model, fits perfectly into a procedural language without such complication. I've even seen it done several times as a library. But its implementation, done well, requires a significant runtime complexity, and I can understand why some folks would prefer not to build that into their system. It's important, though, whatever concurrency model you provide, to do it exactly once, because an environment providing multiple concurrency implementations can be problematic. Go of course solved that issue by putting it in the language, not a library.

There's probably a whole talk to give about these matters, but that's enough for now.

[End of aside]

Another value of concurrency was that it made Go seem like something new.  As I said, some other languages had supported it before, but they were never mainstream, and Go's support for concurrency was a major attractor that helped grow early adoption, pulling in programmers that hadn't used concurrency before but were intrigued by its possibilities.

And that's where we made two significant mistakes.

Whispering gophers (Cooperating Sequential Processes)

First, concurrency is fun and we were delighted to have it, but the use cases we had in mind

were mostly server stuff, meant to be done in key libraries such as net/http, and not everywhere in every program.  And so when many programmers played with it, they struggled to work out how it really helped them.  We should have explained up front that what concurrency support in the language really brought to the table was simpler server software.  That problem space mattered to many but not to everyone who tried Go, and that lack of guidance is on us.

The related second point is that we took too long to clarify the difference between parallelism - supporting multiple computations in parallel on a multicore machine - and concurrency, which is a way to structure code to do that well.

Concurrency is not parallelism

Countless programmers tried to make their code faster by parallelizing it using goroutines, and were often baffled by the resulting slowdown. Concurrent code only goes faster when parallelized if the underlying problem is intrinsically parallel, like serving HTTP requests. We did a terrible job explaining that, and the result baffled many programmers and probably drove some away.

To address this, in 2012 I gave a talk at Waza, Heroku's developer conference, called, Concurrency is not Parallelism. It's a fun talk but it should have happened earlier.

Apologies for that. But the good point still stands: Go helped popularize concurrency as a way to structure server software.

Interfaces

It's clear that interfaces are, with concurrency, a distinguishing idea in Go. They are Go's answer to objected-oriented design, in the original, behavior-focused style, despite a continuing push by newcomers to make structs carry that load.

Making interfaces dynamic, with no need to announce ahead of time which types implement them, bothered some early critics, and still irritates a few, but it's important to the style of programming that Go fostered.  Much of the standard library is built upon their foundation, and broader subjects such as testing and managing dependencies rely heavily on their generous, "all are welcome" nature.

I feel that interfaces are one of the best-designed things in Go.

Other than a few early conversations about whether data should be included in their definition, they arrived fully formed on literally the first day of discussions.

A GIF decoder: an exercise in Go interfaces (Rob Pike and Nigel Tao 2011)

And there is a story to tell there.

On that famous first day in Robert's and my office, we asked the question of what to do about polymorphism. Ken and I knew from C that qsort could serve as a difficult test case, so the three of us started to talk about how our embryonic language could implement a type-safe sort routine.

Robert and I came up with the same idea pretty much simultaneously: using methods on types to provide the operations that sort needed. That notion quickly grew into the idea that value types had behaviors, defined as methods, and that sets of methods could provide interfaces that functions could operate on. Go's interfaces arose pretty much right away.

sort.Interface

That's something that is not often not acknowledged: Go's sort is implemented as a function that operates on an interface. This is not the style of object-oriented programming most people were familiar with, but it's a very powerful idea.

That idea was exciting for us, and the possibility that this could become a foundational

programming construct was intoxicating.  When Russ joined, he soon pointed out how I/O would fit beautifully into this idea, and the library took place rapidly, based in large part on the three famous interfaces: empty, Writer, and Reader, holding an average of two thirds of a method each.  Those tiny methods are idiomatic to Go, and ubiquitous.

The way interfaces work became not only a distinguishing feature of Go, they became the way we thought about libraries, and generality, and composition. It was heady stuff.

But we might have erred in stopping the conversation there.

You see, we went down this path at least in part because we had seen too often how generic programming encouraged a way of thinking that tended to focus on types before algorithms. Early abstraction instead of organic design. Containers instead of functions.

We defined generic containers in the language proper - maps, slices, arrays, channels - without giving programmers access to the genericity they contained. This was arguably a mistake. We believed, correctly I still think, that most simple programming tasks could be handled just fine by those types. But there are some that cannot, and the barrier between what the language provided and what the user could control definitely bothered some people.

In short, although I wouldn't change a thing about how interfaces worked, they colored our thinking in ways it took more than a decade to correct. Ian Taylor pushed us, from early on, to face this problem, but it was quite hard to do given the presence of interfaces as the bedrock of Go programming.

Critics often complained we should just do generics, because they are "easy", and perhaps they can be in some languages, but the existence of interfaces meant that any new form of polymorphism had to take them into account. Finding a way forward that worked well with the rest of the language required multiple attempts, several aborted implementations, and many hours, days, and weeks of discussion. Eventually we roped in some type theorists to help out, led by Phil Wadler.  And even today, with a solid generic model in the language, there are still lingering problems to do with the presence of interfaces as method sets.

Generic sort specification

The final answer, as you know, was to design a generalization of interfaces that could absorb more forms of polymorphism, transitioning from "sets of methods" to "sets of types". It's a subtle but profound move, one that most of the community seems to be fine with, although I suspect the grumbling will never stop.

Sometimes it takes many years to figure something out, or even to figure out that you can't quite figure it out. But you press on.

By the way, I wish we had a better term than "generics", which originated as the term for a different, data-structure-centric style of polymorphism. "Parametric polymorphism" is the proper term for what Go provides, and it's an accurate one, but it's an ugly mouthful. But "generics" is what we say, even though it's not quite right.

The Compiler

One of the things that bothered the programming language community was that the early Go compiler was written in C. The proper way, in their opinion, was to use LLVM or a similar toolkit, or to write the compiler in Go itself, a process called self-hosting.  We didn't do either of these, for several reasons.

First, bootstrapping a new language requires that at least the first steps towards its compiler must be done in an existing language. For us, C was the obvious choice, as Ken had written a C compiler already, and its internals could serve well as the basis of a Go compiler. Also, writing a compiler in its own language, while simultaneously developing the language, tends to result in a language that is good for writing compilers, but that was not the kind of language we were after.

The early compiler worked. It bootstrapped the language well. But it was a bit of an odd duck, in effect a Plan 9-style compiler using old ideas in compiler writing, rather than new ones such as static single assignment.  The generated code was mediocre, and the internals were not pretty.  But it was pragmatic and efficient, and the compiler code itself was modest in size and familiar to us, which made it easy to make changes quickly as we tried new ideas. One critical step was the addition of segmented stacks that grew automatically. This was very easy to add to our compiler, but had we been using a toolkit like LLVM, the task of integrating that change into the full compiler suite would have been infeasible, given the required changes to the ABI and garbage collector support.

Another area that worked well was cross-compilation, which came directly from the way the original Plan 9 compiler suite worked.

Doing it our way, however unorthodox, helped us move fast. Some people were offended by this choice, but it was the right one for us at the time.

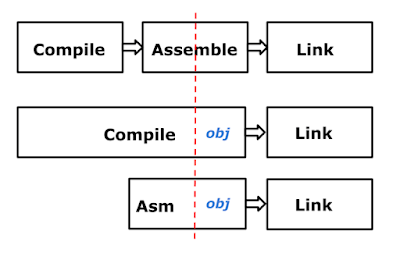The Go compiler architecture post Go 1.5

For Go version 1.5, Russ wrote a tool to translate the compiler semi-automatically from C to Go. By then the language was complete, and concerns about compiler-directed language design were irrelevant. There are talks online about this process that are worth a look. I gave one talk at GopherCon in 2016 about the assembler, which is something of a high point in my lifelong quest for portability.

The Design of the Go Assembler (GopherCon 2016)

We did the right thing by starting in C, but eventually translating the compiler to Go has allowed us to bring to its development all the advantages that Go has, including testing, tooling, automatic rewriting, performance analysis, and so on. The current compiler is much cleaner than the original and generates much better code. But, of course, that is how bootstrapping works.

Remember, our goal was just not a language, but much more.

Our unusual approach was in no way an insult to LLVM or anyone in the language community. We just used the tool that best suited our task. And of course, today there is an LLVM-hosted compiler for Go, and many others, as there should be.

Project Management

We knew from the start that to succeed, Go had to be an open source project. But we also knew that it would be more productive to develop in private until we had the key ideas figured out and a working implementation. Those first two years were essential to clarifying, free of distraction, what we were trying to achieve.

The transition to open source was a huge change, and educational. The input from the community was overwhelming. Engaging with the community took a lot of time and effort, especially for Ian, who somehow found time to answer every question anyone asked. But it also brought so much more. I still marvel at how quickly the Windows port arrived, done entirely by the community under the guidance of Alex Brainman. That was amazing.

It took us a long time to understand the implications of the switch to an open source project, and how to manage it.

In particular, it's fair to say it took us too long to understand the best way to work with the community. A theme throughout this talk is poor communication on our part - even as we thought we were communicating well - and a lot of time was wasted due to misunderstandings and mismatched expectations. It could have been better done.

In time, though, we convinced the community, at least the part that stayed with us, that some of our ideas, although different from the usual open source way, were valuable. The most important were around our insistence on maintaining high code quality through mandatory code review and exhaustive attention to detail.

Mission Control (drawing by Renee French)

Some projects work differently, accepting code quickly and then cleaning up once it's been committed. The Go project works the other way around, trying to get the quality first. I believe that's the more efficient way, but it pushes more work back on the community and they need to understand the value or they will not feel as welcome as they should. There is still much to learn here, but I believe things are much better these days.

By the way, there's a historical detail that's not widely known. The project has had 4 different content management systems: SVN, Perforce, Mercurial and then Git. Russ did a Herculean job of keeping all the history alive, so even today the Git repo contains the earliest changes as they were made in SVN. We all believe it's valuable to keep the history around, and I thank him for doing the heavy lifting.

One other point. People often assume Google tells the Go team what to do. That's simply not true. Google is incredibly generous in its support for Go, but does not set the agenda. The community has far more input. Google has a huge internal Go code base that the team uses to test and verify releases, but this is done by importing from the public repo into Google, not the other way around. In short, the core Go team is paid by Google but they are independent.

Package Management

The process of developing package management for Go was not done well. The package design in the language itself was excellent, I believe, and consumed a large amount of time in the first year or so of our discussions. The SPLASH talk I mentioned earlier explains in detail why it works the way it does if you're interested.

A key point was the use of a plain string to specify the path in an import statement, giving a flexibility that we were correct in believing would be important. But the transition from having only a "standard library" to importing code from the web was bumpy.

Fixing the cloud (drawing by Renee French)

There were two issues.

First, those of us on the core Go team early on were familiar with how Google worked, with its monorepo and everyone building at head. But we didn't have enough experience using a package manager with lots of versions of packages and the very difficult problems trying to resolve the dependency graph. To this day, few people really understand the technical complexities, but that is no excuse for our failure to grapple with those problems from the start. It's especially embarrassing because I had been the tech lead on a failed project to do something similar for Google's internal build, and I should have realized what we were up against.

deps.dev

My work on deps.dev was a something of a penance.

Second, the business of engaging the community to help solve the dependency management problem was well-intentioned, but when the final design came out, even with plenty of documentation and writing about the theory, many in the community felt slighted.

pkg.go.dev

This failing was a lesson to the team in how engagement with the community should really work, and much has improved since as a result.

Things are settled now, though, and the design that emerged is technically excellent and appears to be working well for most users. It just took too long and the road was bumpy.

Documentation and Examples

Another thing we didn't get right up front was the documentation. We wrote a lot of it, and thought we did a good job, but it soon became clear that the community wanted a different level of documentation than we expected.

Gophers fixing a Turing machine (drawing by Renee French)

The key missing piece was examples of even the simplest functions. We thought that all you needed to do was say what something did; it took us too long to accept that showing how to use it was even more valuable.

Executable examples

That lesson was learned, though. There are plenty of examples in the documentation now, mostly provided by open source contributors. And one thing we did very early was make them executable on the web. I gave a talk at Google I/O in 2012 that showed concurrency in action, and Andrew Gerrand wrote a lovely bit of web goo that made it possible to run the snippets right from the browser. I doubt that was the first time it had ever been done, but Go is a compiled language and many in the audience had never seen that trick before. The technology was then deployed to the blog and to the online package documentation.

The Go playground

Perhaps even more important was its deployment to the Go playground, a freely available open sandbox for people to try things out, and even develop code.

Conclusion

We have come a long way.

Looking back, it's clear many things were done right, and they all helped Go succeed. But much could have been done better, and it's important to own up to those and learn from them. There are lessons on both sides for anyone hosting a significant open source project.

I hope that my historical tour of the lessons and their causes will be helpful, and perhaps serve as a sort of apology/explanation for those who objected to what we were doing and how we were doing it.

GopherConAU 2023 mascot by Renee French

But here we are, 14 years after the launch. And it's fair to say that overall it's a pretty good place.

Largely because of the decisions made through the design and development of Go as a way to write software - not just as a programming language - we have arrived somewhere novel.

We got here in part because of:

a strong standard library that implements most of the basics needed for server codeconcurrency as a first-class component of the languagean approach based on composition rather than inheritancea packaging model that clarifies dependency managementintegrated fast build and testing toolsrigorous consistent formattinga focus on readability over clevernessa compatibility guarantee

And, most of all, because of the support of an unbelievably helpful and diverse community of Gophers.

A diverse community (drawings by @tenntenn)

Perhaps the most interesting consequence of these matters is that Go code looks and works the same regardless of who's writing it, is largely free of factions using different subsets of the language, and is guaranteed to continue to compile and run as time goes on. That may be a first for a major programming language.

We definitely got that right.

Thank you.

In May 2009, Google hosted an internal "Design Wizardry" panel, with talks by Jeff Dean, Mike Burrows, Paul Haahr, Alfred Spector, Bill Coughran, and myself. Here is a lightly edited transcript of my talk. Some of the details have aged out, but the themes live on, now perhaps more than ever.

---

Simplicity is better than complexity.

Simpler things are easier to understand, easier to build, easier to debug, and easier to maintain. Easier to understand is the most important, because it leads to the others. Look at the web page for google.com. One text box. Type your query, get useful results. That's brilliantly simple design and a major reason for Google's success. Earlier search engines had much more complicated interfaces. Today they have either mimicked ours, or feel really hard to use.

That's google.com. But what about what's behind it? What about GWS? How you do you invoke it? I looked at the argument list of a running GWS (Google Web Server) instance. XX,XXX characters of configuration flags. XXX arguments. A few name backend machines. Some configure backends. Some enable or disable properties. Most of them are probably correct. I guarantee some of them are wrong or at least obsolete.

So, here's my question: How can the company that designed google.com be the same company that designed GWS? The answer is that GWS configuration structure was not really designed. It grew organically. Organic growth is not simple; it generates fantastic complexity. Each piece, each change may be simple, but put together the complexity becomes overwhelming.

Complexity is multiplicative. In a system, like Google, that is assembled from components, every time you make one part more complex, some of the added complexity is reflected in the other components. It's complexity runaway.

It's also endemic.

Many years ago, Tom Cargill took a year off from Bell Labs Research to work in development. He joined a group where every subsystem's code was printed in a separate binder and stored on a shelf in each office. Tom discovered that one of those subsystems was almost completely redundant; most of its services were implemented elsewhere. So he spent a few months making it completely redundant. He deleted 15,000 lines of code. When he was done, he removed an entire binder from everybody's shelf. He reduced the complexity of the system. Less code, less to test, less to maintain. His coworkers loved it.

But there was a catch. During his performance review, he learned that management had a metric for productivity: lines of code. Tom had negative productivity. In fact, because he was so successful, his entire group had negative productivity. He returned to Research with his tail between his legs.

And he learned his lesson: complexity is endemic. Simplicity is not rewarded.

You can laugh at that story. We don't do performance review based on lines of code.

But we're actually not far off. Who ever got promoted for deleting Google code? We revel in the code we have. It's huge and complex. New hires struggle to grasp it and we spend enormous resources training and mentoring them so they can cope. We pride ourselves in being able to understand it and in the freedom to change it.

Google is a democracy; the code is there for all to see, to modify, to improve, to add to. But every time you add something, you add complexity. Add a new library, you add complexity. Add a new storage wrapper, you add complexity. Add an option to a subsystem, you complicate the configuration. And when you complicate something central, such as a networking library, you complicate everything.

Complexity just happens and its costs are literally exponential.

On the other hand, simplicity takes work—but it's all up front. Simplicity is very hard to design, but it's easier to build and much easier to maintain. By avoiding complexity, simplicity's benefits are exponential.

Pardon the solipsism but look at the query logging system. It's far from perfect but it was designed to be—and still is—the only system at Google that solves the particular, central problem it was designed to solve. Because it is the only one, it guarantees stability, security, uniformity of use, and all the economies of scale. There is no way Google would be where it is today if every team rolled out its own logging infrastructure.

But the lesson didn't spread. Teams are constantly proposing new storage systems, new workflow managers, new libraries, new infrastructure.

All that duplication and proliferation is far too complex and it is killing us because the complexity is slowing us down.

We have a number of engineering principles at Google. Make code readable. Make things testable. Don't piss off the SREs. Make things fast.

Simplicity has never been on that list. But here's the thing: Simplicity is more important than any of them. Simpler designs are more readable. Simpler code is easier to test. Simpler systems are easier to explain to the SREs, and easier to fix when they fail.

Plus, simpler systems run faster.

Notice I said systems there, not code. Sometimes—not always—to make code fast you need to complicate it; that can be unavoidable. But complex systems are NEVER fast—they have more pieces and their interactions are too poorly understood to make them fast. Complexity generates inefficiency.

Simplicity is even more important than performance. Because of the multiplicative effects of complexity, getting 2% performance improvement by adding 2% complexity—or 1% or maybe even .1%—isn't worth it.

But hold on! What about our Utilization Code Red?

We don't have utilization problems because our systems are too slow. We have utilization problems because our systems are too complex. We don't understand how they perform, individually or together. We don't know how to characterize their interactions.

The app writers don't fully understand the infrastructure.

The infrastructure writers don't fully understand the networks.

Or the apps for that matter. And so on and so on.

To compensate, everyone overprovisions and adds zillions of configuration options and adjustments. That makes everything even harder to understand.

Products manage to launch only by building walls around their products to isolate them from the complexity—which just adds more complexity.

It's a vicious cycle.

So think hard about what you're working on. Can it be simpler? Do you really need that feature? Can you make something better by simplifying, deleting, combining, or sharing? Sit down with the groups you depend on and understand how you can combine forces with them to design a simpler, shared architecture that doesn't involve defending against each other.

Learn about the systems that already exist, and build on them rather than around them. If an existing system doesn't do what you want, maybe the problem is in the design of your system, not that one.

If you do build a new component, make sure it's of general utility. Don't build infrastructure that solves only the problems of your own team.

It's easy to build complexity. In the rush to launch, it's quicker and easier to code than to redesign. But the costs accumulate and you lose in the long run.

The code repository contains 50% more lines of code than it did a year ago. Where will we be in another year? In 5 years?

If we don't bring the complexity under control, one day it won't be a Utilization Code Red. Things will get so complex, so slow, they'll just grind to a halt. That's called a Code Black.

 I studied physics in university, and at one point asked a professor if I should learn German, because it seemed all the key texts of early 20th century physics were written by German-speaking physicists in German journals such as Annalen der Physik. But my prof assured me that was not needed, insisting that my own native language would serve me well. And he knew German, so his advice seemed sincere.

In the end he was right, but I still have an occasional pang of regret about never learning another language well enough. Wouldn't it be nice to read Einstein in the original? The E=mc² paper is astonishing in its precision and brevity even in translation. (Although later physicists have criticisms of it, it remains a marvel). I did eventually pick up a bit of German, but not enough for Einstein.

Which brings me to Max Planck, who first quantized light, or so I was told.

By the third year of undergraduate physics, I had been taught the same derivation of the resolution of the "ultraviolet catastrophe" at least three times. The classical (19th century) physics theory of a black body was clearly incomplete because the energy emitted was unbounded: higher and higher frequencies of light (the "ultraviolet")  contributed ever more energy to the solution, leading to infinite energy regardless of the temperature (the "catastrophe"). By quantizing the light, Planck tamped down the runaway energy because as the wavelength increased, the energy of the required to fill the quantized slots (photons) was no longer available, and the spectrum died down, as it does in the real world.

By third or maybe fourth or fifth rendering of this story in class, I began to wonder: Why is the story always told this way? Why is the derivation always exactly the same? It almost seemed like a "just so" story, with the conclusion leading the analysis rather than the other way around. (But read on.) Or perhaps some pedagogue found a nice way to explain the theory to students, and that story was copied from textbook to textbook ad infinitum, eventually to become the story of the invention of quantum mechanics. In short, I was being taught a way to understand the physics, which is fine, but not how the ideas came to life, which left me wanting.

I wanted to investigate by going back to the original paper by Planck. But I couldn't read German, and as far as I knew there was no English translation of the original.

I visited my prof after class and asked him if he would help. He enthusiastically agreed, and we went off to the library to find the appropriate issue of Annalen der Physik. Fittingly, the paper was published in 1900.

Slowly, we—mostly he—worked our way through the paper. It was delightfully, completely, and utterly a 19th-century answer, not the 20th century one that was taught. Planck used thermodynamics, the jewel in the crown of 19th century physics, to derive the black body formula and create the 20th century. The argument was based on entropy, not energy. It had nothing to do, explicitly at least, with photons. But by focusing on the entropy of a set of indistinguishable oscillators at distinct frequencies, he could derive the correct formula in just a few pages. It was a tour de force of thermodynamic reasoning.

Why not teach us the historical derivation? The answer was now clear: This was a deep argument by a towering figure of 19th century physics, one that was beautiful but not a good fit for a 20th century, quantum-capable mind. Yes, Planck quantized the energy, but he did it as a mathematical trick, not a physics one. It was Einstein 5 years later, in his paper on the photoelectric effect, who made photons real by asserting that the quantization was not mere mathematics but due to a real, physical particle (or wave!). Us lowly students were being taught in a world that had photons already in place. Planck had no such luxury.

Another point I learned later, through the books of Abraham Païs, was that Planck knew the formula before he started. Using brilliantly precise experimental work by people in his laboratory, he recognized that the black body spectrum had a shape that he could explain mathematically. It required what we would now call quantization, a distribution over distinct states. In one evening, he found a way to derive that formula from the physics. It was not a matter of quantizing and finding it worked; quite the reverse. The analysis did in fact start from the conclusion, but not as we had been taught.

It's a lovely side detail that Einstein's Nobel Prize was for the photoelectric effect, not relativity as many assumed it would be at the time. The old guard that decided the prizes thought was safe to give it to Einstein for his explanation, based on ideas by Planck, of a different vexing physics problem. That relativity stuff was too risqué just yet. In retrospect, making the photon real was probably Einstein's greatest leap, even though Planck and others of his generation were never comfortable with it. The Nobel committee got it right by accident.

To put all this together, what we learn through our education has always been filtered by those who came after the events. It can be easier to explain things using current ideas, but it's easy to forget that those who invented the ideas didn't have them yet. The act of creating them may only be well understood by stepping back to the time they were working.

I'm sorry I don't remember the professor's name. Our unpicking of the black body story was one of the most memorable and informative days of my schooling, and I will be forever grateful for it.

Color blindness is an inaccurate term. Most color-blind people can see color, they just don't see the same colors as everyone else.

There have been a number of articles written about how to improve graphs, charts, and other visual aids on computers to better serve color-blind people. That is a worthwhile endeavor, and the people writing them mean well, but I suspect very few of them are color-blind because the advice is often poor and sometimes wrong. The most common variety of color blindness is called red-green color blindness, or deuteranopia, and it affects about 6% of human males. As someone who has moderate deuteranopia, I'd like to explain what living with it is really like.

The answer may surprise you.

I see red and green just fine. Maybe not as fine as you do, but just fine. I get by. I can drive a car and I stop when the light is red and go when the light is green. (Blue and yellow, by the way, I see the same as you. For a tiny fraction of people that is not the case, but that's not the condition I'm writing about.)

If I can see red and green, what then is red-green color blindness?

To answer that, we need to look at the genetics and design of the human vision system. I will only be writing about moderate deuteranopia, because that's what I have and I know what it is: I live with it. Maybe I can help you understand how that impairment—and it is an impairment, however mild—affects the way I see things, especially when people make charts for display on a computer.

There's a lot to go through, but here is a summary. The brain interprets signals from the eye to determine color, but the eye doesn't see colors. There is no red receptor, no green receptor in the eye. The color-sensitive receptors in the eye, called cones, don't work like that. Instead there are several different types of cones with broad but overlapping color response curves, and what the eye delivers to the brain is the difference between the signals from nearby cones with possibly different color response. Colors are what the brain makes from those signals.

There are also monochromatic receptors in the eye, called rods, and lots of them, but we're ignoring them here. They are most important in low light. In bright light it's the color-sensitive cones that dominate.

For most mammals, there are two color response curves for cones in the eye. They are called warm and cool, or yellow and blue. Dogs, for instance, see color, but from a smaller palette than we do. The color responses are determined, in effect, by pigments in front of the light receptors, filters if you will. We have this system in our eyes, but we also have another, and that second one is the central player in this discussion.

We are mammals, primates, and we are members of the branch of primates called Old World monkeys. At some point our ancestors in Africa moved to the trees and started eating the fruit there. The old warm/cool color system is not great at spotting orange or red fruit in a green tree.  Evolution solved this problem by duplicating a pigment and mutating it to make a third one. This created three pigments in the monkey eye, and that allowed a new color dimension to arise, creating what we now think of as the red/green color axis. That dimension makes fruit easier to find in the jungle, granting a selective advantage to monkeys, like us, who possess it.

It's not necessary to have this second, red/green color system to survive. Monkeys could find fruit before the new system evolved. So the red/green system favored monkeys who had it, but it wasn't necessary, and evolutionary pressure hasn't yet perfected the system. It's also relatively new, so it's still evolving. As a result, not all humans have equivalent color vision.

The mechanism is a bit sloppy. The mutation is a "stutter" mutation, meaning that the pigment was created by duplicating the original warm pigment's DNA and then repeating some of its codon sequences. The quality of the new pigment—how much the pigment separates spectrally from the old warm pigment—is determined by how well the stutter mutation is preserved. No stutter, you get just the warm/cool dimension, a condition known as dichromacy that affects a small fraction of people, almost exclusively male (and all dogs). Full stutter, you get the normal human vision with yellow/blue and red/green dimensions. Partial stutter, and you get me, moderately red-green color-blind. Degrees of red-green color blindness arise according to how much stutter is in the chromosome.

Those pigments are encoded only on the X chromosome. That means that most males, being XY, get only one copy of the pigment genes, while most females, being XX, get two. That means that if an XY male inherits a bad X, a likely result if he has a color-blind father, he will be color-blind too. An XX female, though, will be much less likely to get two bad copies. But some will get a good one and a bad one, one from the mother and one from the father, giving them four pigments. Such females are called tetrachromatic and have a richer color system than most of us, even than normal trichromats like you.

The key point about the X-residence of the pigment, though, is that men are much likelier than women to be red-green color-blind.

Here is a figure from an article by Denis Baylor in an essay collection called Colour Art & Science, edited by Trevor Lamb and Janine Bourriau, an excellent resource.

The top diagram shows the pigment spectra of a dichromat, what most mammals have. The bottom one shows the normal trichromat human pigment spectra. Note that two of the pigments are the same as in a dichromat, but there is a third, shifted slightly to the red. That is the Old World monkey mutation, making it possible to discriminate red. The diagram in the middle shows the spectra for someone with red-green color blindness. You can see that there are still three pigments, but the difference between the middle and longer-wave (redder) pigment is smaller.

A deuteranope like me can still discriminate red and green, just not as well. Perhaps what I see is a bit like what you see when evening approaches and the color seems to drain from the landscape as the rods begin to take over. Or another analogy might be what happens when you turn the stereo's volume down: You can still hear all the instruments, but they don't stand out as well.

It's worth emphasizing that there is no "red" or "green" or "blue" or "yellow" receptor in the eye. The optical pigments have very broad spectra. It's the difference in the response between two receptors that the vision system turns into color.

In short, I still see red and green, just not as well as you do. But there's another important part of the human visual system that is relevant here, and it has a huge influence on how red-green color blindness affects the clarity of diagrams on slides and such.

It has to do with edge detection. The signals from receptors in the eye are used not only to detect color, but also to detect edges. In fact since color is detected largely by differences of spectral response from nearby receptors, the edges are important because that's where the strongest difference lies. The color of a region, especially a small one, is largely determined at the edges.

Of course, all animals need some form of visual processing that identifies objects, and edge detection is part of that processing in mammals. But the edge detection circuitry is not uniformly deployed. In particular, there is very little high-contrast detection capability for cool colors. You can see this yourself in the following diagram, provided your monitor is set up properly. The small pure blue text on the pure black background is harder to read than even the slightly less saturated blue text, and much harder than the green or red. Make sure the image is no more than about 5cm across to see the effect properly, as the scale of the contrast signal matters:

In this image, the top line is pure computer green, the next is pure computer red, and the bottom is pure computer blue. In between is a sequence leading to ever purer blues towards the bottom. For me, and I believe for everyone, the bottom line is very hard to read.

Here is the same text field as above but with a white background:

Notice that the blue text is now easy to read. That's because it's against white, which includes lots of light and all colors, so it's easy for the eye to build the difference signals and recover the edges. Essentially, it detects a change of color from the white to the blue. Across the boundary the level of blue changes, but so do the levels red and green. When the background is black, however, the eye depends on the blue alone—black has no color, no light to contribute a signal, no red, no green—and that is a challenge for the human eye.

Now here's some fun: double the size of the black-backgrounded image and the blue text becomes disproportionately more readable:

Because the text is bigger, more receptors are involved and there is less dependence on edge detection, making it easier to read the text. As I said above, the scale of the contrast changes matters. If you use your browser to blow up the image further you'll see it becomes even easier to read the blue text.

And that provides a hint about how red-green color blindness looks to people who have it.

For red-green color-blind people, the major effect comes from the fact that edge detection is weaker in the red/green dimension, sort of like blue edge detection is for everyone. Because the pigments are closer together than in a person with regular vision, if the color difference in the red-green dimension is the only signal that an edge is there, it becomes hard to see the edge and therefore hard to see the color. 

In other words, the problem you have reading the blue text in the upper diagram is analogous to how much trouble a color-blind person has seeing detail in an image with only a mix of red and green. And the issue isn't between computer red versus computer green, which are quite easy to tell apart as they have very different spectra, but between more natural colors on the red/green dimension, colors that align with the naturally evolved pigments in the cones.

In short, color detection when looking at small things, deciding what color an item is when it's so small that only the color difference signal at the edges can make the determination, is worse for color-blind people. Even though the colors are easy to distinguish for large objects, it's hard when they get small.

In this next diagram I can easily tell that in the top row the left block is greenish and the right block is reddish, but in the bottom row that is a much harder distinction for me to make, and it gets even harder if I look from father away, further shrinking the apparent size of the small boxes. From across the room it's all but impossible, even though the colors of the upper boxes remain easy to identify.

Remember when I said I could see red and green just fine? Well, I can see the colors just fine (more or less). But that is true only when the object is large enough that the color analysis isn't being done only by edge detection. Fields of color are easy, but lines and dots are very hard.

Here's another example. Some devices come with a tiny LED that indicates charging status by changing color: red for low battery, amber for medium, and green for a full charge. I have a lot of trouble discriminating the amber and green lights, but can solve this by holding the light very close to my eye so it occupies a larger part of the visual field. When the light looks bigger, I can tell what color it is.

Another consequence of all this is that I see very little color in the stars. That makes me sad.

Remember this is about color, just color. It's easy to distinguish two items if their colors are close but their intensities, for example, are different. A bright red next to a dull green is easy to spot, even if the same red dulled down to the level of the green would not be. Those squares above are at roughly equal saturations and intensities. If not, it would be easier to tell which is red and which is green.

To return to the reason for writing this article, red/green color blindness affects legibility. The way the human vision system works, and the way it sometimes doesn't work so well, implies there are things to consider when designing an information display that you want to be clearly understood.

First, choose colors that can be easily distinguished. If possible, keep them far apart on the spectrum. If not, differentiate them some other way, such as by intensity or saturation.

Second, use other cues if possible. Color is complex, so if you can add another component to a line on a graph, such as a dashed versus dotted pattern, or even good labeling, that helps a lot.

Third, edge detection is key to comprehension but can be tricky. Avoid difficult situations such as pure blue text on a black background. Avoid tiny text.

Fourth, size matters. Don't use the thinnest possible line. A fatter one might work just as well for the diagram but be much easier to see and to identify by color.

And to introduce one last topic, some people, like me, have old eyes, and old eyes have much more trouble with scattered light and what that does to contrast. Although dark mode is very popular these days, bright text on a black background scatters in a way that makes it hard to read. The letters have halos around them that can be confusing. Black text on a white background works well because the scatter is uniform and doesn't make halos. It's fortunate that paper is white and ink is black, because that works well for all ages.

The most important lesson is to not assume you know how something appears to a color-blind person, or to anyone else for that matter. If possible, ask someone you know who has eyes different from yours to assess your design and make sure it's legible. The world is full of people with vision problems of all kinds. If only the people who used amber LEDs to indicate charge had realized that.

(Another resurrected post from the my old Google stream, which appeared on or about Dec 6, 2011.)

For unknown reasons, someone asked me if had a copy of this file today. I didn't, but I remembered it was in dmr's home directory, and asked a friend there to find it. I remembered correctly. I don't know why it was touched in 1993, but the .v (mips object file) was created in late 1992. I leave the significance of that date as an exercise for the reader.

By the way, sizeof(void) is illegal, so I'm unsure how it was compiled; my friend assures me the compilers from then didn't accept it either.

Because G refuses to leave the indentation alone and screws up the ls formatting, I'm posting a screen grab here, but i'll include the source code, poorly formatted and rudely scrubbed of indentation, so you can play with the bytes. Just for fun, after the first screen grab I'll post a second screen grab of this post in edit mode before I hit save.

#include <u.h>
#include <libc.h>

typedef int ☺☹☻;
typedef void ☹☺☻;
enum
{
    ☹☻☺ = sizeof(☺☹☻),
    ☻☺☹ = sizeof(☹☺☻),
};

☹☺☻
main(☹☺☻)
{
    ☺☹☻ ☺☻☹;

    for(☺☻☹=☻☺☹; ☺☻☹<☹☻☺; ☺☻☹ )
        print("☺☻☹ = %d\n", ☺☻☹);
    exits(☻☺☹);
}

(Another resurrected post from the my old Google+ stream, which appeared on or about Sep 4, 2012. Thirty years of age isn't too far off now.)


UTF-8 turned 20 years old yesterday.

It's been well documented elsewhere (http://www.cl.cam.ac.uk/~mgk25/ucs/utf-8-history.txt) that one Wednesday night, after a phone call from X/Open, Ken Thompson and I were sitting in a New Jersey diner talking about how best to represent Unicode as a byte stream. Given the experience we had accumulated dealing with the original UTF, which had many problems, we knew what we wanted. X/Open had offered us a deal: implement something better than their proposal, called FSS/UTF (File System Safe UTF; the name tells you something on its own), and do so before Monday. In return, they'd push it as existing practice.

UTF was awful. It had modulo-192 arithmetic, if I remember correctly, and was all but impossible to implement efficiently on old SPARCs with no divide hardware. Strings like "/*" could appear in the middle of a Cyrillic character, making your Russian text start a C comment. And more. It simply wasn't practical as an encoding: think what happens to that slash byte inside a Unix file name.

FSS/UTF addressed that problem, which was great. Big improvement though it was, however, FSS/UTF was more intricate than we liked and lacked one property we insisted on: If a byte is corrupted, it should be possible to re-synch the encoded stream without losing more than one character. When we claimed we wanted that property, and sensed we could press for a chance to design something right, X/Open gave us the green light to try.

The diner was the Corner Café in New Providence, New Jersey. We just called it Mom's, to honor the previous proprietor. I don't know if it's still the same, but we went there for dinner often, it being the closest place to the Murray Hill offices. Being a proper diner, it had paper placemats, and it was on one of those placemats that Ken sketched out the bit-packing for UTF-8. It was so easy once we saw it that there was no reason to keep the placemat for notes, and we left it behind. Or maybe we did bring it back to the lab; I'm not sure. But it's gone now.

I'll always regret that.

But that's my only regret in this story. UTF-8 has made the world a better place and I am delighted to have been a facilitator in its creation.

So tonight, please give a toast to a few quickly sketched boxes on a placemat in a New Jersey diner that today define how humans represent their text to be sent across international boundaries (http://googleblog.blogspot.com/2012/02/unicode-over-60-percent-of-web.html), and especially to the X/Open folks for giving us the chance and the Unicode consortium and IETF for pushing it so successfully.

Signed,
-rob
U+263A '☺' white smiling face

(Here's the next resurrected post, this time from Jun 8, April 30, 2012.)

A while back I posted the questions from the 1984 Unix/mpx Exit quiz: https://commandcenter.blogspot.com/2020/01/unix-quiz.html

Here they are again, with annotated answers. The answers are in the form of the simplified pattern that the mpx exit program used to verify them.

Note: I have never seen a correct set of answers posted on line except when they originated from this list. In other words, I don't believe anyone ever got all the questions correct, even with a web search engine. It may not even be possible.

1. Q:The source code motel: your source code checks in, but it never checks out. What is it?
A:sccs
The Source Code Control System. The reference is to the Roach Motel.

2. Q:  Who wrote the first Unix screen editor?
A: irons
Ned Irons wrote a full-screen editor (the first?) at IDA in the 1960s and a Unix version, perhaps a translation, at Yale a few years later.

3. Q:  Using TSO is like kicking a {what?} down the beach.
A: dead whale
The quote is from Steve Johnson. For those of you who never experienced TSO, it's an accurate characterization.

4. Q:  What is the filename created by the original dsw(1)?
A: core
Setting the file's i-number using the switches on the front panel was the other half of its user interface.

5. Q:  Which edition of Unix first had pipes?
A: third | 3
Look it up.

6. Q:  What is =O=?
A: empire
Empire was a large-scale strategy game developed at Reed College and made a computer game by Peter Langston (and perhaps others?).

7. Q:  Which Stephen R. Bourne wrote the shell?
A: software | 1138 | regis
There were two people named Stephen R. Bourne working at SGI in the early 1980s. The one who wrote software (as opposed to designing hardware), who had worked in BTL Center 1138, or whose middle name was Regis: he wrote the shell.

8. Q:  Adam Buchsbaum's original login was sjb. Who is sjb?
A: sol & buchsbaum
Adam was one of many Unix room kids with parents who worked at the Bell Labs. Adam was unusual because his father was executive vice president but apparently didn't have enough clout to get his kid his own login.

9. Q:  What was the original processor in the Teletype DMD-5620?
A: mac & 32
The 5620 was the productized Blit. Trick question: most people thought the 5620, like the Blit, had a 68000 but it used the much less suitable yet more expensive BELLMAC-32.

10. Q:  What was the telephone extension of the author of mpx(2)?
A: 7775
The (2) here is important. Greg Chesson wrote mpx(2); I wrote mpx(8).

11. Q:  Which machine resulted in the naming of the "NUXI problem"?
A: series 1 | series one
The IBM Series/1 was big-endian. Swap the bytes of "UNIX", the first text printed as Unix booted.

12. Q:  What customs threat is dangerous only when dropped from an airplane?
A: belle | chess machine
Ken Thompson took Belle (the chess machine) to the Soviet Union for a tour. Well, he tried: the machine was impounded by U.S. customs and never left American soil. Ken's trip was not much fun.

13. Q:  Who wrote the Bourne Shell?
A: bourne
The only real gimme in the list. Feels like a trick question though.

14. Q:  What operator in the Mashey shell was replaced by "here documents"?
A: pump
Sometimes better ideas do win out.

15. Q:  What names appear on the title page of the 3.0 manual?
A: dolotta & petrucelli & olsson
This refers to System 3, two before System V. It always makes your technology seem more modern when you use Roman numerals.

16. Q:  Sort the following into chronological order: a) PWB 1.2, b) V7, c) Whirlwind, d) System V, e) 4.2BSD, f) MERT.
A: cagbef
Whirlwind is a ringer.

17. Q:  The CRAY-2 will be so fast it {what?} in 6 seconds.
A: infinite | np-complete | p=np
What can I say? The whole exercise was juvenile.

18. Q:  How many lights are there on the front panel of the original 11/70?
A: 52
We counted.

19. Q:  What does FUBAR mean?
A: failed unibus address register
It's really a register name on the VAX-11/780. Someone at DEC liked us.

20. Q:  What does "joff" stand for?
A: jerq obscure feature finder
Tom Cargill's debugger changed its name soon after we were pressured by management to change Jerq to Blit.

21. Q:  What is "Blit" an acronym of?
A: nothing
Whatever people thought, even those who insisted on spelling it BLIT, Blit was not an acronym.

22. Q:  Who was rabbit!bimmler?
A: rob
See Chapter 1 of The Unix Programming Environment for another theory.

23. Q:  Into how many pieces did Ken Thompson's deer disintegrate?
A: three | 3
During takeoff at Morristown airport, propeller meets deer; venison results.

24. Q:  What name is most common at USENIX conferences?
A: joy | pike
Sun Microsystems made these obnoxious conference badges that said, "The Joy of UNIX". We retaliated.

25. Q:  What is the US patent number for the setuid bit?
A: 4135240
Dennis Ritchie was granted the only patent that came out of Research Unix.

26. Q:  What is the patent number that appears in Unix documentation?
A: 2089603
I'm not a fan of this stuff. Look it up yourself.

27. Q:  Who satisfied the patent office of the viability of the setuid bit patent?
A: faulkner
At a time when software patents were all but unknown, Roger Faulkner demonstrated to a judge that the patent was sufficiently well explained by taking a Unix kernel without it and putting it in, given the patent text. A clean-room recreation, if you will.

28. Q:  How many Unix systems existed when the Second Edition manual was printed?
A: 10 | ten
It's right there in the introduction.

29. Q:  Which Bell Labs location is HL?
A: short hills
Easy for Labbers, not so easy for others. MH was Murray Hill.

30. Q:  Who mailed out the Sixth Edition tapes?
A: biren | irma
Packages from Irma Biren were very popular in some circles.

31. Q:  Which University stole Unix by phone?
A: waterloo
Software piracy by modem. I'm not telling.

32. Q:  Who received the first rubber chicken award?
A: mumaugh
I don't remember what this was about, and the on-line references are all about this quiz.

33. Q:  Name a feature of C not in Kernighan and Ritchie.
A: enum | structure assignment | void
K&R (pre-ANSI) was pretty old.

34. Q:  What company did cbosg!ccf work for?
A: weco | western
Western Electric. Chuck Festoon was created by Ron Hardin as a political statement about automated document processing.

35. Q:  What does Bnews do?
A: suck | gulp buckets
Obscure now, but this was a near-gimme at the time.

36. Q:  Who said "Sex, Drugs, and Unix?"
A: tilson
Mike Tilson handed out these badges at an earlier USENIX. They were very popular, although the phrase doesn't scan in proper Blockhead style.

37. Q:  What law firm distributed Empire?
A: dpw | davis&polk&wardwell
Peter Langston worked for this Manhattan law firm, whose computer room had a charming view of FDR Drive.

38. Q:  What computer was requested by Ken Thompson, but refused by management?
A: pdp-10 | pdp10
Sic.

39. Q:  Who is the most obsessed private pilot in USENIX?
A: goble | ghg
Cruel but fair.

40. Q:  What operating system runs on the 3B-20D?
A: dmert | unix/rtr
DMERT gives you dial tone. The D stands for dual, as in dual-processor for redundancy. In a particular Bell System way, it was an awesome machine.

41. Q:  Who wrote find(1)?
A: haight
Dick Haight also wrote cpio(1), which to my knowledge was the first Unix program that did nothing at all unless you gave it options.

42. Q:  In what year did Bell Labs organization charts become proprietary?
A: 83
And soon after, PJW appeared.

43. Q:  What is the Unix epoch in Cleveland?
A: 1969 & dec & 31 & 19:00
Easy.

44. Q:  What language preceded C?
A: nb
Between B and C was NB. B was interpreted and typeless. NB was compiled and barely typed. C added structs and became powerful enough to rewrite the Unix kernel.

45. Q:  What language preceded B?
A: bon | fortran
BCPL is not the right answer.

46. Q:  What letter is mispunched by bcd(6)?
A: r
This trick question was used to verify that a Unix knock-off was indeed a clean-room reimplementation. Or maybe they just fixed the bug.

47. Q:  What terminal does the Blit emulate?
A: jerq
Despite what Wikipedia claims at the time I'm writing this, the Blit did not boot up with support for any escape sequences.

48. Q:  What does "trb" stand for (it's Andy Tannenbaum's login)?
A: tribble
I honestly never knew why this moniker was applied to Andy (no, the other one), although I can guess.

49. Q:  allegra!honey is no what?
A: lady
Peter Honeyman is many things, but ladylike, no.

50. Q:  What is the one-line description in vs.c?
A: screw works interface
From the man page for the driver for the Votrax speech synthesizer.

51. Q:  What is the TU10 tape boot for the PDP-11/70 starting at location 100000 octal?
A: 012700 172526 010040 012740 060003 105710 012376 005007
It's in the book. There was a sad time when I not only had this memorized, it was in muscle memory.

52. Q:  What company owns the trademark on Writer's Workbench Software?
A: at & t communications
AT&T never could decide what it was to call itself.

53. Q:  Who designed Belle?
A: condon | jhc
Joe Condon, hardware genius, died just a few months ago. Belle was the first computer to achieve international master status, using (roughly speaking) Joe's hardware and Ken's software.

54. Q:  Who coined the name "Unix"?
A: kernighan | bwk
This one is well known.

55. Q:  What manual page mentioned Urdu?
A: typo
I miss the typo command and occasionally think of recreating it.

56. Q:  What politician is mentioned in the Unix documentation?
A: nixon
The Nixon era was a dark period for people maintaining time zone tables.

57. Q:  What program was compat(1) written to support?
A: zork | adventure
My memory is rusty on this one and I don't have the 6th Edition manual to hand.

58. Q:  Who is "mctesq"?
A: michael & toy & esquire
Michael Toy wrote rogue...

59. Q:  What was "ubl"?
A: rogue | under bell labs
... which Peter Weinberger renamed ubl when he imported it. The renaming made sense to anyone who worked at Murray Hill.

60. Q:  Who bought the first commercial Unix license?
A: rand
The RAND Corporation led the way.

61. Q:  Who bought the first Unix license?
A: columbia
Columbia University.

62. Q:  Who signed the Sixth Edition licenses?
A: shahpazian
He was the lawyer who literally signed off on the licenses.

63. Q:  What color is the front console on the PDP-11/45 (exactly)?
A: puce
That's what DEC called it. It's not puce at all, which is why it's a good trivia question.

64. Q:  How many different meanings does Unix assign to '.'?
A: lots | many | countless | myriad | thousands
Ken's favorite character on the keyboard.

65. Q:  Who said "Smooth rotation butters no parsnips?"
A: john & tukey
John Tukey discovered/invented the Fast Fourier Transform algorithm, coined the term "bit" for Claude Shannon, and of course uttered this unforgettable gem.

66. Q:  What was the original name for cd(1)?
A: ch
You answered chdir, didn't you? You were wrong.

67. Q:  Which was the first edition of the manual to be typeset?
A: 4 | four
The old phototypesetter was much smellier than a modern printer.

68. Q:  Which was the first edition of Unix to have standard error/diagnostic output?
A: 5 | five
The idea came remarkably late. Also, back then shell scripts bound standard input to the script, not the terminal.

69. Q:  Who ran the first Unix Support Group?
A: maranzano
USG was a force for internal and commercial Unix development in AT&T.

70. Q:  Whose Ph.D. thesis concerned Unix paging?
A: ozalp & babaoglu
The name was well known; the trick was spelling it correctly when you were in a hurry to get home.

71. Q:  Who (other than the obvious) designed the original Unix file system?
A: canaday
Rudd Canaday was there at the beginning.

72. Q:  Who wrote the PWB shell?
A: mashey
John Mashey, inventor of the pump operator.

73. Q:  Who invented uucp?
A: lesk
In so doing, Mike Lesk created the job category of (amateur) network operations engineer.

74. Q:  Who thought of PWB?
A: evan ivie
Evan Ivie pushed on the Software Tools metaphor to instigate the Programmer's Workbench. It feels quaint now.

75. Q:  What does grep stand for?
A: global regular expressions print
I've read countless incorrect etymologies for 'grep'. It's just the ed command g/re/p. The reference here is the spelling on the original man page. That final 's' is key to getting this one right.

76. Q:  What hardware device does "dsw" refer to?
A: console & 7
The profound "delete from switches" program was in its purest form on the PDP-7 in the First Edition.

77. Q:  What was the old name of the "/sys" directory?
A: ken
Ken and...

78. Q:  What was the old name of the "/dev" directory?
A: dmr
... Dennis divided their work this way until the Seventh Edition.

79. Q:  Who has written many random number generators, but never one that worked?
A: ken | thompson
Sorry, Ken, but it's true and you know it.

80. Q:  Where was the first Unix system outside 127?
A: patent
The Bell Labs patent office truly benefited from automated document processing made possible in the early versions of Research Unix. I believe they started using it when the kernel was still in assembler.

81. Q:  What was the first Unix network?
A: spider
You thought it was Datakit, didn't you? But Sandy Fraser had an earlier project.

82. Q:  What was the original syntax for ls -l | pr -h?
A: ls -l>"pr -h"> | <"ls -l"Notation is important. Ken's introduction of the pipe symbol (not to be confused with the | of the pattern here) was a masterstroke.

83. Q:  Why is there a comment in the shell source /* Must not be a register variable */?
A: registers & longjmp
You should be able to understand this.

84. Q:  What is it you're not expected to understand?
A: 6 | 5 & process
What's amazing to me now is hard this was to understand, let alone to invent, yet within a few years we all realized it could be done almost trivially with setjmp and longjmp.p.p1 {margin: 0.0px 0.0px 0.0px 0.0px; font: 14.0px 'Lucida Grande Mono550'; color: #000000} span.s1 {font-variant-ligatures: no-common-ligatures}

(Here's another resurrected post from April 30, 2012. Answers in a followup.)


People objected that there was no Exit item on the main menu for the mpx program that put windows on the Blit; see http://en.wikipedia.org/wiki/Blit_(computer_terminal) (which mistakenly says it implemented cursor addressing when turned on - as if!) and http://www.cs.bell-labs.com/cm/cs/doc/83/mpx.ps.gz. It seemed unnecessary, since you could just power cycle. Why clutter the menu? (Those were simpler times.)

After hearing too much complaining, I decided to implement Exit, but did it a special way. Late one night, with help from Brian Redman (ber) and Pat Parseghian (pep), I cranked out a set of trivia questions to drive the Exit control. Answer the question right, you can exit; get it wrong, you're stuck in mpx for a little longer. To make this worthwhile, the questions had to be numerous and hard, and had to be verified by the machine, so the quiz code included a little pattern matcher. It also had to be tiny, since the machine only had 256KB and the display took 100KB of that. (Those were simpler times.)

The response was gratifying. I'll never forget seeing someone, who shall remain nameless, a vociferous complainer about the lack of Exit, burble with excitement when he saw the menu item appear, only to crumble in despair when the question arrived. I forget which question it was, but it doesn't matter: they're all hard.

The questions were extended by lots of suggestions from others in the Unix lab, and then in 1984 they were handed out as a bloc in a trivia contest at the USENIX conference in Salt Lake City. To quote an observer, "The submission with the most correct answers (60) was from a team comprising David Tilbrook, Sam Leffler, and presuambly others. Jim McKie had the best score for an individual (57) and was awarded an authenticated 1972 DECtape containing Unix Version 2. Finally, Ron Gomes had 56 correct answers and received an original engraved "Bill Joy" badge, which once belonged to Bill himself, from Sun Microsystems." That score of 57 was so impressive we hired Jim a little later, but that's another story.

How much Unix trivia do you know? Test your mettle; the questions appear below. This may be one of the hardest quizzes ever to originate outside of King William's College.

I've disabled comments because people will just send in spoilers. If you want to discuss or collaborate, do so elsewhere. I'll publish the computer-readable, pattern-matching answers here in a few days.

Good luck, and may your TU-10 never break your 9-track boot tape.

-rob


1. The source code motel: your source code checks in, but it never checks out. What is it?
2. Who wrote the first Unix screen editor?
3. Using TSO is like kicking a {what?} down the beach.
4. What is the filename created by the original dsw(1)?
5. Which edition of Unix first had pipes?
6. What is =O=?
7. Which Stephen R. Bourne wrote the shell?
8. Adam Buchsbaum's original login was sjb. Who is sjb?
9. What was the original processor in the Teletype DMD-5620?
10. What was the telephone extension of the author of mpx(2)?
11. Which machine resulted in the naming of the "NUXI problem"?
12. What customs threat is dangerous only when dropped from an airplane?
13. Who wrote the Bourne Shell?
14. What operator in the Mashey shell was replaced by "here documents"?
15. What names appear on the title page of the 3.0 manual?
16. Sort the following into chronological order: a) PWB 1.2, b) V7, c) Whirlwind, d) System V, e) 4.2BSD, f) MERT.
17. The CRAY-2 will be so fast it {what?} in 6 seconds.
18. How many lights are there on the front panel of the original 11/70?
19. What does FUBAR mean?
20. What does "joff" stand for?
21. What is "Blit" an acronym of?
22. Who was rabbit!bimmler?
23. Into how many pieces did Ken Thompson's deer disintegrate?
24. What name is most common at USENIX conferences?
25. What is the US patent number for the setuid bit?
26. What is the patent number that appears in Unix documentation?
27. Who satisfied the patent office of the viability of the setuid bit patent?
28. How many Unix systems existed when the Second Edition manual was printed?
29. Which Bell Labs location is HL?
30. Who mailed out the Sixth Edition tapes?
31. Which University stole Unix by phone?
32. Who received the first rubber chicken award?
33. Name a feature of C not in Kernighan and Ritchie.
34. What company did cbosg!ccf work for?
35. What does Bnews do?
36. Who said "Sex, Drugs, and Unix?"
37. What law firm distributed Empire?
38. What computer was requested by Ken Thompson, but refused by management?
39. Who is the most obsessed private pilot in USENIX?
40. What operating system runs on the 3B-20D?
41. Who wrote find(1)?
42. In what year did Bell Labs organization charts become proprietary?
43. What is the Unix epoch in Cleveland?
44. What language preceded C?
45. What language preceded B?
46. What letter is mispunched by bcd(6)?
47. What terminal does the Blit emulate?
48. What does "trb" stand for (it's Andy Tannenbaum's login)?
49. allegra!honey is no what?
50. What is the one-line description in vs.c?
51. What is the TU10 tape boot for the PDP-11/70 starting at location 100000 octal?
52. What company owns the trademark on Writer's Workbench Software?
53. Who designed Belle?
54. Who coined the name "Unix"?
55. What manual page mentioned Urdu?
56. What politician is mentioned in the Unix documentation?
57. What program was compat(1) written to support?
58. Who is "mctesq"?
59. What was "ubl"?
60. Who bought the first commercial Unix license?
61. Who bought the first Unix license?
62. Who signed the Sixth Edition licenses?
63. What color is the front console on the PDP-11/45 (exactly)?
64. How many different meanings does Unix assign to '.'?
65. Who said "Smooth rotation butters no parsnips?"
66. What was the original name for cd(1)?
67. Which was the first edition of the manual to be typeset?
68. Which was the first edition of Unix to have standard error/diagnostic output?
69. Who ran the first Unix Support Group?
70. Whose Ph.D. thesis concerned Unix paging?
71. Who (other than the obvious) designed the original Unix file system?
72. Who wrote the PWB shell?
73. Who invented uucp?
74. Who thought of PWB?
75. What does grep stand for?
76. What hardware device does "dsw" refer to?
77. What was the old name of the "/sys" directory?
78. What was the old name of the "/dev" directory?
79. Who has written many random number generators, but never one that worked?
80. Where was the first Unix system outside 127?
81. What was the first Unix network?
82. What was the original syntax for ls -l | pr -h?
83. Why is there a comment in the shell source /* Must not be a register variable */?
84. What is it you're not expected to understand?