Jordan Ellenberg's Blog
February 27, 2026
Networking and granfallooning
It has come to my attention that students at prestigious universities are referring to the practice of cold-emailing alums of their school and asking for Zoom calls to discuss possible summer internships as “networking.”
No! It is not!
“Networking” is called networking because it involves a network: the collection of strong and loose ties of various kinds between pairs of people. When an older friend from your prestigious college, who has graduated and now works at presitigious corporation X, puts in a word for you with her boss, that is networking; you’re connected to your friend, your friend is connected to her boss, you are in the same connected component of and indeed at rather short distance in the network. “Networking” means making use of the (hopefully) rich neighborhood of iterated ties that is supposed to develop organically when you move among other ambitious people who are going places, some of them places you also want to go.
A list of other alumni of your prestigious college is not a network. It is just a set. Totally different mathematical object. More precisely, it is a granfalloon. (Vonnegut specifically names “Cornell alumni” as an example!) Granfallooning is not networking.
February 25, 2026
In which I rescue Harvard’s grading system
The Harvard faculty is proposing to hard-cap A’s at 20% per course, leading to an undergraduate crashout the good old Yard has not seen the likes of since,the dining hall discontinued the Chickwich.
I am in cold hard print telling people not to worry about grade inflation. I think I was right about grade inflation as it was in 2002. The situation of grading at Harvard now, on the other hand, gives even me pause. Half the class having GPAs of 3.8 or above is probably too much.
Still, the current argument leaves me with nobody to really root for. When a Harvard student says “We pay to go here to get the product, which is to have a better signal of performance… If you’re just lowering that for everyone, then you’re just lowering the value you provide as a business for the same cost, even while raising tuition year over year,” I just want to cry in my soup a little bit. Is Harvard a product and a business? Sure. But is it just that? And is the product being purchased really “a better signal of performance?” Another undergrad has a slightly different spin on the new policy, and on the point of college: “It misses the point of college, which is to network, go out there, have fun…It would create so much pressure where life wouldn’t be worth that much to live.”
Again: is that the point of college? Is it, specifically, the point of Harvard? It is a point of Harvard, that I’ll grant you. I networked there. I had fun. I believe I probably did whatever is meant these days by “going out there.” But I also went to class, and made a point of really trying a lot, both in the areas that would become my job and those (painting, poetry, Biblical interpretation, the politics of the Chinese Cultural Revolution) which weren’t and were never going to be. That, too, is a point of Harvard.
Anyway: this hubbub is all a bit rich considering the Monterey Jack-level mildness of the proposed policy. The faculty wants to limit the proportion of A grades to 20% — or more precisely, 20% of the class + 4, so small seminars could still have a solid complement of A’s. (Maybe this entire thing is secretly a plan to incentivize grade-grubbing undergrads to take a seminar once in a while?) But no other grade would be limited; a professor would be free to give 80% A- and 20% A if they saw fit. And 20% A’s isn’t a return to the pre-Vietnam gentleman’s C era; it would be roughly in line with grading practices in 2006, at which time, as far as I know, life at Harvard was considered worth living.
But I don’t think the faculty’s document supporting the plan is very convincing either. The ostensible problem to be solved is that the present system offers no way for really excellent students to distinguish themselves, that grades have ceased to offer any meaningful signal at all. Is that true? That median 3.8-ish GPA translates into about half A’s and half A-‘s in your 32 college credits. The difference between straight A’s and 16 A’s and 16 A-‘s is actually pretty noticeable on a transcript!
You can actually see this in the faculty’s own dataset. They propose using APR (average percentile rank) rather than GPA for internal awards. That just means you get a score that averages your rank in each class; if you get the median grade, you get 50, whether that grade was a B or an A- or an A. Look, they say, this is highly correlated with GPA, but no grade inflation!
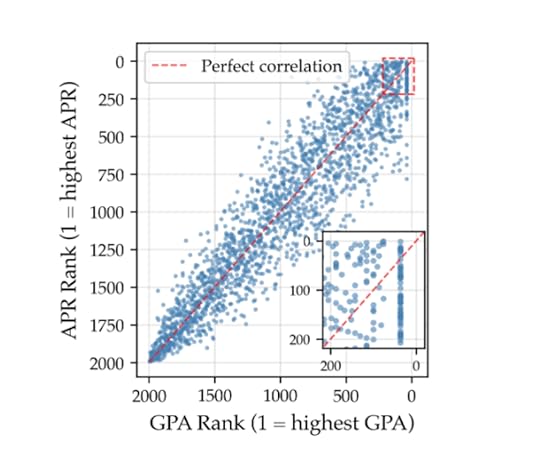
Well, sure — but you can read that same correlation to say maybe GPA isn’t doing such a bad job capturing academic variation among the students!
The report makes much of that vertical line at the far edge — students with 4.0 averages, who are indeed not distinguished from one another by GPA. How are you supposed to know who’s the best of the best of the best? I’m not moved by this argument. The true academic standouts are the ones who are easy, not hard to tell from the grade-grubbing masses. They do things GPA doesn’t measure, and faculty know they did these things, and they write about it in their letters.
(In passing: the faculty also complain that “the shift of the summa cum laude cutoff so close to 4.0 that summa eligibility now depends on GPAs carried out to five decimal places.” How can this be? Getting 32 A’s is a 4.0. Getting 31 As and an A- is just about 3.99. I only need two decimal places to tell those apart! Are students taking tens of thousands of courses and getting an A- in just one?)
The report also makes the claim, several times, that a broader grade range would improve “fairness” in the overall academic assessment. Would it? I can see the argument that the relation between GPA and academic success would be less noisy if the grade range were broader; but I’m not sure how much. More compelling to me is their argument that narrow GPA range gives an advantage to students with strong networks who have access to back-channel endorsements orthogonal to GPA (“A fine touch with the epee, that one, just the sort of man for the job.”) I can look at a 3.8 and 3.9 and see a measurable difference in how well the student did in classes, but to the outside world I will concede those numbers look pretty damned close.
Still, I can’t help feeling that the motivation for the policy is simpler. Professors don’t really believe signs are arbitrarily assigned to the signified. We have a sense of what an A means, and don’t want to give an A for work that’s not A work. But somehow we’re embarrassed to just say that; we have to dress it up in concerns about fairness and credibility and get all scatterplot about it all.
One thing that makes me sad: despite the policy difference between faculty and undergrads, they seem to agree on one big thing; that grades are the reason for students to work. The students worry that with scarcer A’s, they’ll have to work too much; the faculty worry that with too many A’s available, the students aren’t working enough. (This article in Harvard Magazine is a really nice, humane rendition of this view.)
Let me be honest about something at this point. When I was a Harvard undergrad I was a huge grade-grubber. I always knew exactly what my GPA was. I once went to office hours to argue with a very patient sociology TA that my final exam essay was better than he thought it was and how could I possibly be getting a B+? (I got the B+.) So I understand the drive for the grade and I don’t look down on it. (OK, maybe I look down on it a little, but in an “I’ve been there too” kind of way.) But I don’t think the grades were why I was working hard in class. I worked hard because I was there to learn. Not everybody who goes to Harvard is aiming to be a professional scholar, I get that. But my possibly sentimental view of Harvard is that it’s where you go because you want to learn things, in every area, with the same kind of depth and intensity as the scholars-to-be of that thing.
Since I spent this post disagreeing with everyone, and since I do more or less agree that the Harvard grading system isn’t ideal, I ought to tell you what proposal I would have written if I were king of the Harvard faculty! Here is, my three-point plan:
Bring back the 15-point scale. When I was in college, the GPA was out of 15. An A was 15, an A- was 14, a B+ was 12 (see why I was so mad at my sociology TA?) and so on. Harvard undergrads worry that a Harvard with fewer A’s will leave them with lower GPA’s than their competitors from other colleges, and employers and med schools won’t recognize “Harvard grades different.” Under this plan, they would have way higher GPA than kids from other schools! That’s partly a joke but partly not — a completely incompatible scale would make it clear that there was no direct translation. Many schools couldn’t get away with this, but Harvard can. And one of Harvard’s goofy charms is that they call everything by their own Harvard-y names. Political science is “Government.” Dorms are “Houses.” Majors are “concentrations.” Why shouldn’t a 4.0 be a 15?Establish the A+. This option (which is what Princeton does) is brought up in the faculty report only to be rejected. That’s coming from the “A should mean A!” perspective. But an A+ would solve the “how to distinguish really superb performance” problem. You don’t even have to call it an A+ or average it into GPA; you could call it “with distinction,” and there could be a clear understanding that you were only allowed to give one or two per class, that zero distinctions is fine and even expected, and that any student who asked about distinction was disqualified for distinction. A student who racked up three or four in their career would be a visible standout.More pass-fail. I teach a first-year seminar at Wisconsin, a writer’s workshop where the students, mostly data science majors, learn how to write good sentences and put those sentences together into good, clear paragraphs. I am going to be honest; I give mostly A’s in this class. And I stand by that practice, and would be pissed if the dean told me I had to stop, because I’m teaching a hard skill that most first-years don’t feel confident in and I think fewer students would take it if they thought they might get a bad grade for not being a fully developed writer of English prose. I want them to take the risk of coming to my class! The big downside of low grades, for me, is that they might discourage students from signing up for a hard course in an area where they don’t feel fully confident. Those are the exact courses we want students to take! (Sidebar: of course, this is also a potential downside of high grades; if you feel everybody around you has a 4.0, maybe even taking a class where you might get an A- is too great a danger to endure.) My son, as I think I’ve mentioned, goes to Brown, and I think the relaxed culture of taking courses pass-fail there really does help students stretch themselves more. I just looked this up in the student handbook, and it looks like Harvard students are also essentially unlimited in how many of their electives they can take pass-fail. So maybe this is a cultural change that Harvard needs — sure, limit A’s, but also create an Brown-like environment where students are encouraged to take that weird but interesting course with a great professor where you really might not master everything, and take it pass/fail. Heck, Harvard could require every student to take a certain number of pass-fail courses that met no requirement. Imagine the undergraduate crashout that would cause….February 22, 2026
As an old calculus professor of mine used to say
“The Mean Value Theorem — it wears many different sheepskins, but it is always the same wolf.”
I love this, despite not knowing exactly what he meant! It helps to hear it in a Polish accent.
(The professor was Piotr Mikulski.)
February 18, 2026
Waiting for Godot (Gen-X rewrite)
Here’s a good use case for LLMs — they are quite good at recovering the text from files you saved on a Macintosh word processor in the early 90s and have been transporting from computer to computer ever since, despite the fact that they don’t open anymore. Gemini is able to recover the text! In some cases, it even recovers your edits and changes, which it will tell you about, thanks to quirks in the way files were saved in those days. Try it yourself, if you’re a digital hoarder like I am.
Anyway, here’s something I don’t remember writing at all, which based on the folder its in I must have written in 1994, probably right after I saw Reality Bites. I cannot lie, I still think this is pretty funny. Though it’s possible that you have to be exactly the same age as me, and also to have been a childhood devotee of absurdist theater, for this to be a knee-slapper for you. Well, I don’t care, here it is, courtesy of 22-year-old me and Google Gemini 3 Pro.
[Memo/Notes]
Lydia: The kid brought this script home from school, of all places; I think we may have something here. It’s about a couple of Russians or something. I made a few changes and cuts here and there. I’m looking at it as a generation-X kind of project Twentysomething, MTV, etc. Let me know what you think. D.J..“WAITING FOR GODOT” EXT. A COUNTRY ROAD. A TREE — EVENING.
ESTRAGON [Winona Ryder] and VLADIMIR [Ethan Hawke] are sitting in twin BARCA-LOUNGERS, watching a rerun of “HAPPY DAYS.”On soundtrack: “Zooropa.”ESTRAGON is trying to open a beer bottle. She gives up, exhausted, rests, tries again. As before.ESTRAGON: Nothing to be done.VLADIMIR: That bites.ESTRAGON: Not as much as it bites to be born into our generation; a generation that has to live in an environment despoiled by the greed and fast living of our parents, that’s supposed to find jobs in the recessionary market their failed economic policies created, that lacks any moral or spiritual guideposts beyond their hypocritical ’60s so-called “rebellion!”VLADIMIR: What?ESTRAGON: Nothing.SILENCE.VLADIMIR: This place sucks. I hate watching TV outside.ESTRAGON: Then let’s leave.VLADIMIR: We can’t.ESTRAGON: Why not?VLADIMIR: We’re waiting for Godot.ESTRAGON: Who’s Godot?VLADIMIR: The drummer in my band.ESTRAGON: Cool![Executive Note]
[Lydia: after this there was some stuff about Christ which seemed a little off the topic, so I cut it. When we come back they’re still in the same place.][Scene Continues]
On soundtrack: “In Your Eyes.”VLADIMIR: (weepy) God, Estragon… It’s just like that episode of the Brady Bunch where Peter has to do a school project on the Pilgrims, and the Bradys all get together to do a movie, and they want to make snow to show how hard the Pilgrim’s winter was, and Alice throws Frosted Flakes off the garage, and in the end even though they fought all through it Peter’s teacher says how it really demonstrated community winning out over adversity, and gives him an A+…ESTRAGON: It was Bobby.VLADIMIR: Peter.ESTRAGON: Bobby.VLADIMIR: (angrily) You’re a liar like the Isuzu guy.ESTRAGON: Not!VLADIMIR: (weepy again) Anyway… I just want the teacher to come out at the end of the half hour and give me an A+ even though all I’ve got is Frosted Flakes… All I’ve got is damn Frosted Flakes!CLOSE of ESTRAGON- soulful. CLOSE of VLADIMIR- also soulful. They have SEX.EXT. A COUNTRY ROAD. A TREE NIGHT
ESTRAGON and VLADIMIR are back in the Barca-Loungers. ESTRAGON is again trying vainly to open the beer bottle. On soundtrack: “Zooropa.”ESTRAGON: Nothing to be done.Enter POTSY [Anson Williams] and LUCKY [Molly Ringwald]. POTSY is leading LUCKY on a rope; he carries a whip.VLADIMIR: Potsy! We love you, man!ESTRAGON: We have an ironic drinking game where we compete to name the most episodes of “Happy Days!”VLADIMIR: You’re so bad… you’re good!POTSY: (shouts) SILENCE!SILENCE. Potsy tugs Lucky’s chain, making her HOWL.POTSY: (to Lucky) Think, pig!He jerks her chain again. On soundtrack: “Pretty in Pink.”POTSY: THINK, PIG!LUCKY: Given the existence as uttered forth in the public works of Judd Nelson of Emilio Estevez of Ally Sheedy quaquaquaqua the trademark sneer the trademark sneer in the public works of John Hughes quaquaquaqua more or less Duran Duran Duran Duran in the public works of Andrew McCarthy more or less a function of parachute pants of break dancing of the sitting president of break dancing as can be seen in the quaquaquaqua the trademark sneer as can be seen in the public works of Captain Lou Albano has lately been seen has lately been seen as more or less a function of the sitting president… break dancing… the sneer… the sneer…VLADIMIR: What a couple of losers.ESTRAGON and VLADIMIR drive Potsy and Lucky away with a hail of stones.ESTRAGON: Potsy totally sold out. I’m so depressed…VLADIMIR: He really melts in your hand not in your mouth. When we needed it good, he had it bad. Bet he could eat just one.ESTRAGON: What?VLADIMIR: Nothing.ESTRAGON: Nothing to be done.[Executive Note]
[Lydia Are you seeing this line like I am? Tag line for trailers definite potential to become “slacker” catchphrase- talk to SNL? -D.J.][Scene Continues]
SILENCE.VLADIMIR: This place sucks.ESTRAGON: Then let’s leave.VLADIMIR: We can’t.ESTRAGON: Why not?VLADIMIR: We’re waiting for Godot. We were supposed to have rehearsal an hour ago.ESTRAGON: What a lame-ass. Let’s go find him.VLADIMIR: Good idea.EXT. NEW YORK CITY, OUTSIDE CBGB– NIGHT
Vladimir and Estragon have found GODOT.[Lydia can we get Evan Dando? D.J.]GODOT: Sorry I was late… but I was getting us this amazing gig! There’s scouts here from every major record company.. and MTV! And guess what… we’re opening for PEARL JAM!VLADIMIR: COOL!INT. CBGB
Vladimir, Godot, and the band are pouding through a furious “grunge” rendition of “Zooropa.” We pan through the crowd, noticing various PROMOTERS eagerly preparing contracts. Shot settles on Estragon, who’s standing in the back, not dancing. CLOSE- ESTRAGON crying tears of joy.ESTRAGON: I’m glad we didn’t wait!CREDITS.[Executive Note]
[D.J. It’s a go. Anything for the kids. Lydia.]February 16, 2026
Yankees Outright Yanquiel Fernandez
How could they do this to a guy whose name literally means “Yankee of God?”
February 10, 2026
Luck or loveliness
So pretty.
I like the life I’ve had but also in some ways I wish I had been in New Zealand playing with the Tall Dwarfs in 1981 instead of being a 10-year-old in the suburbs of Washington, DC.
February 6, 2026
Now pitching, Cadeler Wellvich
Barring any last-minute moves, and despite being linked to just about every big-name pitcher on the free-agent market, the Orioles will go into 2026 as they left 2025, without a clear #1 starter. Depth, though, they have — the list of plausible back-of-the rotation starting pitchers on the team is a long one. What do you do when you have too many 5s and not enough 1s?
Here’s an idea. One imagines Kyle Bradish, Trevor Rogers, Shane Baz, and Dean Kremer are locked in for rotation spots. Zach Eflin, too, but he may still be recovering from his latest injury when the season starts. So who’s our #5 starter in April 2026? I think it ought to be Cade Povich and Tyler Wells. Povich gets the first four innings, Wells the next four, then it’s Ryan Helsley time. Doesn’t this make a lot of sense? Both these guys are a lot worse their second time through the order. (Povich career splits, Wells career splits.) So if each one’s facing 15 batters you’re getting more of the best of them and you’d expect their overall performance to be better than either has been as a standard starter. Maybe 5 +5 = 3! Plus: the lefty-righty switch messes up any opposition attempt to maintain a platoon advantage. And while Wells was great in four starts at the end of last year, he’s historically been better in relief, which this role, technically, would be.
Yes, you’re using six roster spots for starters, but you probably need fewer relief innings in the games Wellvich starts. Maybe this way Povich and Wells pitch 80 innings each instead of Povich pitching 110 as the 5th starter and Wells pitching 60 in long relief; not that much difference in the number of innings needing coverage by the bullpen minus Wells.
February 4, 2026
George Birkhoff, faces made of lines
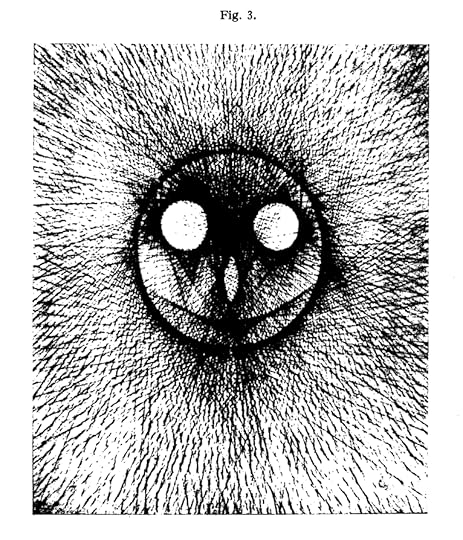
Look at this cutie! This is from a 1940 paper by George Birkhoff. It concerns the question of what pictures can be drawn on a sheet of notebook paper if you can only put straight lines on the page. Alternatively — the nonnegative span of the delta functions of lines form some kind of subspace of the nonnegative functions on the plane, and you can ask which functions are in there . This, which Birkhoff credits to “Mr. David Middleton, a student at Harvard University,” is one of them. The David Middleton in question must surely be this guy, who did a whole oral history interview and never mentioned that he drew faces with straight lines for Birkhoff.
I think it would be hard to publish a paper like this in Jour. Math. Pur. Appl. now. But this is fun! Maybe we’re taking math too seriously and should draw more faces.
February 3, 2026
What’s the entropy of a random integer?
Surely people have thought about this but I couldn’t find anything on a short search.
The question: let n be a random integer, say in [N,2N]. It factors as the product of p_i^a_i. So you can think of the proportion of n that is “made of” the prime p_i to be (a_i log p_i / log n). OK, now this gives you a probability distribution. What’s its entropy?
You can make this a little simpler by restricting to squarefree integers. (Not sure whether this should change the answer.) The sizes of the prime factors of a random squarefree integer are supposed to match the cycle lengths of a random large permutation (say on N letters), so now we can ask that question: break a random permutation up into cycles, which gives another probability distribution; namely, that which assigns each cycle the probability cycle length / N. (This is called the Poisson-Dirichlet process with parameters (0,1). Here’s a Terry T. post about it, and why it governs prime factorizations of random integers.) What’s the entropy of this one?
Well, we can at least guess the average. Let X_i be the number of i-cycles in a random permutation on N letters. Then the X_i are roughly independent Poisson variables of mean 1/i. So there are X_i i-cycles, each appearing with probability i/n, and thus each contributing (-i/N) log (i/N) or (i/N)(log N – log i) to the entropy of the distribution. Now all we have to do is sum over i! You are summing
(i/N) X_i log N – (i/N) X_i log i
over all i. The first sum is easy; the sum of iX_i has to be N, so this is just log N.
What about the subtrahend? This is 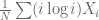 . Since $X_i$ has expected value $1/i$, the expected value of this part should be
. Since $X_i$ has expected value $1/i$, the expected value of this part should be 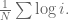
I didn’t tell you how long the sum was! But i certainly can’t be greater than N so let’s stop the sum there. Then the sum of log_i, by Stirling’s formula, is very close to N log N – N. So the second part of the sum is about log N – 1. Almost exact cancellation! Our estimate for the mean entropy is
log N – (log N – 1) = 1.
Is that true? Is it also true for integers? (I did actually run some computations on this and the mean looked less than one, but numbers with only five or six digits are just lousy with primes and near-primes, which could well mess this up.) Does the entropy actually converge to a distribution or does it just have a mean? What about the exponential of the entropy, the so-called perplexity? Does it have a mean? I ask because I tend to think of the perplexity of a probability distribution as roughly “the actual number of possible outcomes if you count them with information in mind.” So you could think of the distribution of perplexity, if there is one, as the information theorist’s version of the Erdos-Kac theorem. “You thought the number of prime factors grew like log log n, Pal and Mark, but come on, some of those primes are so small they barely matter — actually the expected number of prime factors is constant!”
I’m sure this is all well-understood by someone, but as I’ve mentioned before I think a blog is a good place to model the casual way mathematicians think about things in real life, but not always in public.
January 19, 2026
It’s a good old-fashioned Wisconsin booger-freezer out there!
One of my favorite weather sayings. And I ran into a neighbor on my way home from the errand I was running so I got to say it in person, always a treat. 3 degrees Fahrenheit, sunny and windy in Madison right now, really not bad at all. When I moved here I thought Wisconsin winter was going to be a fifth season, a new thing that would test and harden me, but actually there are only a few days like today which are really a different kind of cold than I grew up with on the East Coast, and I’ll be honest, I enjoy them. The cold air reboots your head. I am wearing my biggest, most shapeless sweater, and a scarf in the pattern of the flag of Schiermonnikoog.

If you liked this post you might like Tom Scocca’s weather reviews. I don’t think Tom has ever experienced a good old-fashioned Wisconsin booger-freezer, though.
(Update to this post. “A good old-fashioned something or other” isn’t both good and old-fashioned, it’s a thing characterized as “good old,” which is a semantic unit on its own, and is also old-fashioned. It means something like “good old old-fashioned Wisconsin booger-freezer,” which of course you would not say. Are there any other examples like this, where two two-word phrases which overlap combine into a three-word phrase? It’s kind of like composable morphisms in a category.)
Jordan Ellenberg's Blog
- Jordan Ellenberg's profile
- 421 followers



