David Orrell's Blog
December 31, 2025
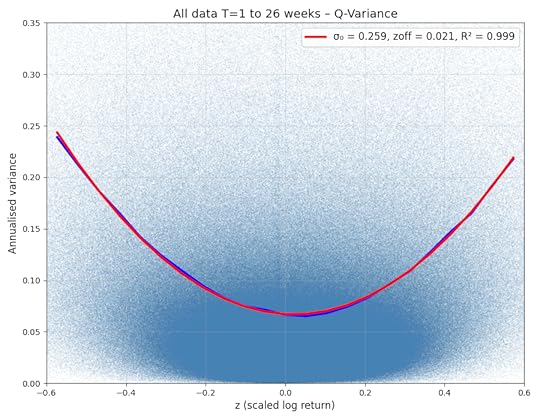
The q-variance challenge
Can any continuous-time model, using no more than three free parameters, reproduce what may be the most clear-cut empirical property of variance, namely the parabolic relationship known as q-variance?
The competition was launched on 8 December 2025 by Wilmott magazine.
Prize: One-year subscription to WILMOTT magazine and publication of the technique.
Competition details: See the GitHub site.
Further model information: Q-Variance: or, a Duet Concerning the Two Chief World Systems. Wilmott 2025 (138)
September 2, 2025
Talking with physicists about quantum finance
Quantum economics/finance is based on the idea that you can use quantum probability to model financial markets. Over the past several years I have had numerous discussions on the topic with physicists, and often (not always) they seem to follow the same track. To save time in future, I will summarise the steps briefly, using the example of a recent discussion with an anonymous online poster at a Wilmott finance forum.
First, I should note that I do have some prior, given that I am myself a physics dropout (though I did stay around long enough to learn some quantum mechanics). As I wrote in my book Apollo’s Arrow: “it seemed that my physics education was acting like a kind of indoctrination, and forcing me to see the world in this very controlling way. Partly as a result of this dramatic flash of insight, I dropped the physics part of the program and switched to mathematics, which leaves applications up to the user – and also allowed me to take film studies as an option.”
Also, I’ll admit that I don’t have too much respect for people who write my ideas off as “definitely not true” and “quantum doodah” under the cover of anonymity. The situation is asymmetric – they know who I am, but if I ever ran into them in person at a conference or something I would never know. And it makes them essentially unaccountable for what they say.
Anyway the conversation, which can be found here (see comments from “katastrofa”) follows a usual path. It begins with some technical points based on confusion about the model, but ends with the assertion that markets aren’t really quantum so quantum methods don’t apply. A few key features:
Physicists are very arrogant when they discuss quantum ideas! (Or maybe they are just assuming the person whose theory is being debunked – the debunkee? – is even more simpleminded than we actually are.) This poster (who appears to be an expert in quantum physics) starts by asking for some clarifications but soon gets straight to explaining my own model to me along with basic ideas from quantum mechanics known to anyone with a minimum background in the topic. For example I learn here that “In the harmonic‑oscillator, after an energy measurement the system is in level n and the position distribution is not Gaussian – it’s a Gaussian multiplied by a squared Hermite polynomial.” So interesting!A normal discussion about a mathematical model would include things like does the model actually fit the data, how many parameters does it need, and so on. Those topics don’t even come up here, because the focus is on debunking theory. For example q-variance states that the average variance over periods T with a price change x is given by sigma^2 + z^2/2 where z=x/sqrt(T). What makes it interesting is that (a) it was a prediction, (b) it is a big effect (total variance is double the minimum variance), (c) it applies for all periods T, be it a few days or a year, (d) no such effect has been reported in the literature, (e) it has obvious implications for things like option pricing (the volatility smile?), and (f) there is no parameter – no adjustable control knob – on the z^2 term. All of this means that the model should be incredibly easy to falsify, which is rare in economics. If people think the model is wrong, you would think the starting point would be to test it using data – but that never comes up (seriously never). Something very wrong there.Physicists find it hard to see quantum probability as a mathematical technique, so they always reframe models as analogies. This person writes of “the analogy … of a quantum harmonic oscillator”, the “analogy to a coherent state”, volatility modes that “themselves are analogous to qho energy levels,” and so on. Since calculus was originally invented to model planetary motion, should we refer to Black-Scholes at all times, not as a mathematical model, but as an analogy to planets?Related to point 1, when a physicist in debunking mode gets something wrong, rather than concede it they simply move on to another point. This can continue for a long time. Here for example the poster fundamentally misunderstands q-variance (they say “the conditional variance rises like a+bx^2, and let’s fix b=1/2 for parsimony”) but when called on it asserts there is no confusion. They then drop the topic of q-variance and switch to making mistakes about the q-distribution (“definitely not true”). This makes the discussion frustrating.It is only when you get near the end of the conversation that the underlying assumptions finally surface: that the wave function is not real (“In markets there’s no literal wavefunction anyway”) so any model based on quantum ideas is “quantum doodah” (or as Murray Gell-Mann called it in a chapter of a book “flapdoodle”). Hate to break it to you physicists, but mathematical models aren’t real either.Finally, the motivations of the modeller (debunkee) are brought into question. The usual idea is that anyone plugging a quantum model is a bit of a charlatan, and quantum ideas are being used as a kind of advertising gimmick to make the model look cool (if so, it is the least successful pitch in the history of advertising). Here, the implication is quite subtle, and the poster only suggests that I am using quantum to make an interesting story: “storytelling can outrun derivation – I’m only asking that the story and the math line up.”Now, sometimes people do change their mind, as this physics professor (who used their real name) did:

Usually though the whole discussion is a waste of time because it is based on an almost religious faith that quantum models aren’t models but represent some deep ontological truth about physics. In other words, exactly the kind of thing that got me out of physics in the first place.
Of course, physicists are often the go-to experts on quantum techniques, so obviously have a lot to contribute. And many leaders in areas such as quantum finance/game theory/cognition and so on are themselves renegade physicists. But it’s not up to physicists to decide what mathematical techniques are suitable for use in the social sciences. And physicists saying that quantum models shouldn’t be applied in other areas is a bit like mathematicians saying that physicists shouldn’t use complex numbers to model probability because they weren’t invented for that.
What I find really ridiculous though is that physicists have all this time to debate quantum models, and so little to say about the obviously flawed assumptions of classical economics. Maybe they could debunk that.
For a discussion of the relationship between quantum economics and physics, see here.
I am always open to good-faith scientific dialogue, but if any physicists out there want to physics-plain quantum at me, a few guidelines:
State your name.State your priors. If you just want to debunk the theory then be up front – I am unlikely to change your mind.Oh, and
If this is about debunking, I hear there are other places on the internet where they are misusing quantum theory so please check them out first.August 12, 2025
Qvar, an online app to explore q-variance
The Qvar Shiny app is now live at:
https://david-systemsforecasting.shinyapps.io/qvar/
The app provides an interactive way to explore q-variance – a property that links price changes and volatility in a way not anticipated by traditional models. It draws on ideas from quantum probability to test whether a universal variance relationship holds across major stocks.
What Is Q-Variance?
In the q-variance framework, the expected variance of log returns x, corrected for drift, over a period T follows to good approximation the formula
V(z)=σ0^2+z^2/2
where z=x∕√T and σ0 is a minimum volatility parameter that is estimated from the data.
This formula implies that variance grows quadratically with the scaled price displacement z, in contrast to the linear time-dependence in classical models such as Black–Scholes. The app illustrates this property for 355 S&P 500 stocks that have been in the index for at least 75% of trading days between 1992-01-02 and 2025-04-17.
What You Can Do in the App
 Pick any of 355 S&P 500 stocks
Pick any of 355 S&P 500 stocks Choose time periods from 1 week to nearly a year
Choose time periods from 1 week to nearly a year Compare actual market behaviour to the q-variance prediction
Compare actual market behaviour to the q-variance prediction Download the raw data to analyse yourself
Download the raw data to analyse yourselfWhy It’s Worth a Look
Reveals patterns hidden in noisy financial dataHelps test whether the quantum-inspired model matches realityUseful for researchers, students, and anyone curious about volatilityMinimum volatility + price-change effect = q-variance
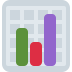
How to Use the App
Plots tab – Choose a stock ticker and range of periods T (1–50 weeks).
The upper plot shows variance vs. z for selected periods.
Points: Variance from individual non-overlapping periods.
Blue line: LOESS interpolation with shaded confidence region.
Red line: Q-variance curve.
The lower plot shows the average for all stocks (grey) compared with the selected stock (black).
Data tab – View/download the time series for the selected stock, including prices and computed variables.
 Try it now:
Try it now:
https://david-systemsforecasting.shinyapps.io/qvar/
See also: QEF15 – A quantum oscillator model of stock markets 2: q-variance and the q-distribution
June 22, 2025
QEF16 – A quantum jump model of option pricing
As seen in QEF15, stock market data follows q-variance and the q-distribution. Q-variance refers to the property that the expected variance of log returns x, corrected for drift, over a period T follows to good approximation the formula V(z)=σ^2+z^2/2 where z=x∕√T. This property follows because we model price change as the displacement of a quantum harmonic oscillator, so a larger displacement is associated with higher energy and therefore higher volatility.
The probability distribution associated with q-variance is a Poisson-weighted sum of Gaussians known as the q-distribution. The Poisson rate parameter is λ=0.5 and the standard deviation for each term is σ_n=σ√(1+2n).
The q-distribution can be used to calculate the price of a call option. We can also use it to calculate the q-implied volatility σ_q, which is the volatility to be used in the Black-Scholes model for this distribution. The answer is seen to be
σ_q^2=q^2 σ^2+(1-q^2 ) z^2
where q≅0.95.
We can therefore compare three kinds of volatility. Q-implied volatility is the number suggested by quantum model. Implied volatility is the number used by traders. Payout-implied volatility is the number which corresponds to average payouts.
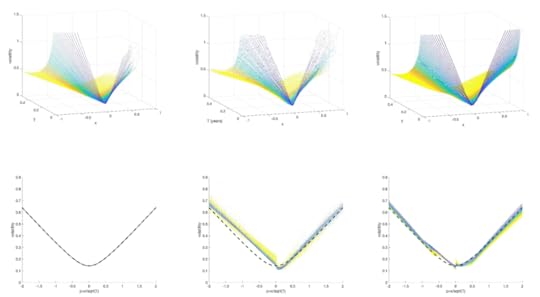 Plots show q-implied (left), implied (middle), and payout-implied (right) volatility
Plots show q-implied (left), implied (middle), and payout-implied (right) volatility as a function of x and T (top row) and z only (bottom row).
To summarise, the q-distribution can be used to calculate the expected payout of a call option. The q-implied volatility (the volatility suggested by the quantum model) is quite close to both implied volatility (the volatility used by traders) and payout-implied volatility (the volatility which reflects average payout)
This suggests that markets follow a quantum distribution, and traders are using a quantum model to price options – they just don’t know it
For further reading, see:
Orrell D (2025) A Quantum of Variance, and the Challenge for Finance. Wilmott 2025(138).
Orrell D (2025) A Quantum Jump Model of Option Pricing. Journal of Derivatives 33(1).
Previous: QEF15 – A quantum oscillator model of stock markets 2: q-variance and the q-distribution
Playlist: Quantum Economics and Finance
QEF15 – A quantum oscillator model of stock markets 2: q-variance and the q-distribution
Q-variance refers to the property, described previously in QEF14, that the expected variance of log returns x, corrected for drift, over a period T follows to good approximation the formula
V(z)=σ^2+z^2/2
where z=x∕√T.
Q-variance follows because we model price change over a period as the displacement of a quantum harmonic oscillator (here we are not explicitly modelling the market maker).
A corollary is that the price change distribution follows a Poisson-weighted distribution of normal curves, where the Poisson rate parameter is λ=0.5, and the standard deviation of the n’th term is σ_n=σ√(1+2n). This distribution, known as the q-distribution, looks like the figure below.
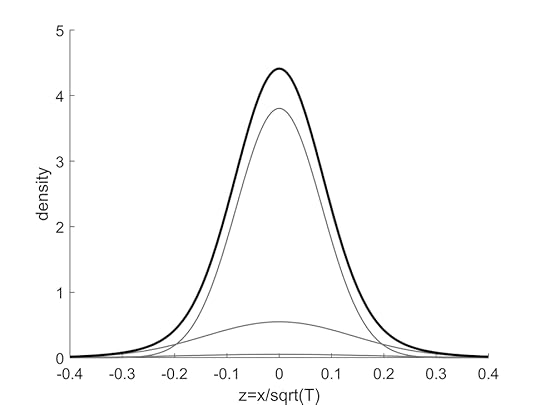 The q-distribution (solid line) is composed of a Poisson-weighted sum of Gaussians. The first three terms are shown by the thin lines.
The q-distribution (solid line) is composed of a Poisson-weighted sum of Gaussians. The first three terms are shown by the thin lines.The q-distribution can be derived in a number of ways. One is to note that the volatility of the perturbed oscillator is computed by measuring the energy level n. The result follows a Poisson distribution, with σ_n being the standard deviation associated with each level. An ensemble of oscillators, representing separate transactions over the period, then gives the q-distribution. Another way to derive the distribution is by demonstrating that the value λ=0.5 is consistent with q-variance.
The test of course is whether q-variance and the associated q-distribution are consistent with data. The figure below shows variance as a function of z=x∕√T for 355 stocks for the period January 1992 to April 2025. For each stock, the results are compiled over periods T of one to 50 weeks. Companies included are currently in the S&P 500 index and have data for at least 75 percent of the period. Blue line is the mean, red line is the quantum model with a small shift to account for effects such as skew.
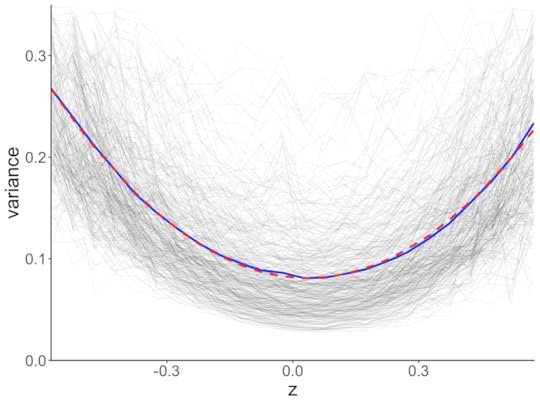 Q-variance
Q-varianceThe left panel in the figure below shows the distribution of z for the same 355 stocks. Blue line is the mean. The right panel shows the same, after the results for each stock are scaled to bring them in line with the mean. The q-distribution, shown by the red dashed line, is almost indistinguishable from the mean.
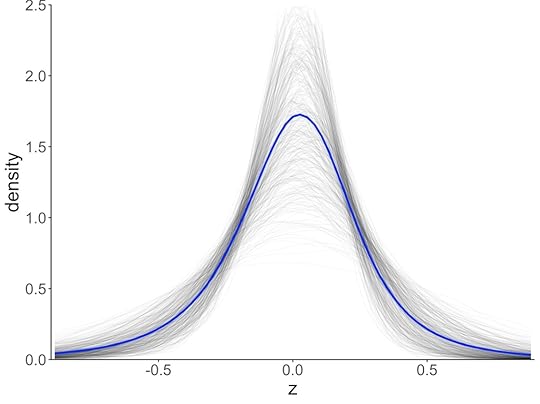
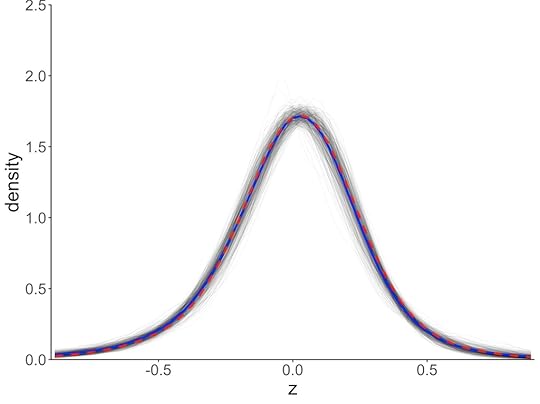 Q-distribution
Q-distributionTo summarise, the quantum oscillator model predicts that variance will show the property of q-variance, and price changes will follow the q-distribution. These are connected because the q-distribution is consistent with q-variance. The predictions have been tested against stock market data and are in excellent agreement with results. However neither q-variance nor the q-distribution are consistent with a classical random walk, which is probably why they have not previously been used in finance
For further reading, see:
Wilmott P and Orrell D (2025) Q-Variance: or, a Duet Concerning the Two Chief World Systems. Wilmott 2025(138).
Orrell D (2025) A Quantum of Variance, and the Challenge for Finance. Wilmott 2025(138).
Previous: QEF14 – Is the volatility smile real or imaginary?
Next: QEF16 – A quantum jump model of option pricing
Playlist: Quantum Economics and Finance
October 2, 2024
Gaia, or how to write the perfect eco-thriller
Back in 2021 I heard about a new film out of South Africa called Gaia. According to the plot synopsis, the story starts with two characters Gabi and Winston exploring a forest in South Africa. When they leave, Gabi tells Winston that “we can’t just leave our trash here.” It then turns out that Winston has been infected by a lethal fungus, which Gabi later links to a Gaia-worshipping survivalist cult.
The movie didn’t achieve wide release, however the reviews were quite good. According to Roger Ebert, “Gaia has a lot to say about humanity’s destruction of the environment, about the ‘tipping point’ we have collectively reached in the Anthropocene, but the film says it with creativity, mad flights of imagination, and even humor.”
My interest though was due to the fact that in 1999 I wrote a screenplay that was also called Gaia. In my version, the story starts with two sisters Sandra and Anne exploring a forest in Venezuela. When they leave, Anne tells Sandra “We shouldn’t leave behind any trace that we were here.” It then turns out that Anne has been infected by a lethal fungus, which Sandra later links to a Gaia-worshipping survivalist cult.
At the time I found an agent with an address on Sunset Boulevard, and had some interest in the screenplay from a UK production firm, but it didn’t go anywhere, so I adapted the screenplay into a novel (represented by the Robert Lecker Agency) and switched my focus to writing non-fiction books on science and economics.
Now, leaving aside the question of whether the South African team had read my book (available in self-published form at Amazon since 2009), and noting that the stories do take very different turns (mine moves to the city and has a much bigger scale, different style etc.), I think that the initial premise which they share is in some ways pretty optimal for an eco-thriller about our relationship with the living planet.
When I wrote my screenplay, the logic of the story was that if the Earth is alive, and humanity is harming it, then the Earth will produce an antibody to counter us, which we will perceive as a disease. The Earth doesn’t make a very good antagonist in a story though, so as a human stand-in I used the leader of an Earth-worshipping cult who plans to spread the disease to save Gaia. Also, the disease can’t just escape and wipe everyone out (end of story) so we need the cult to actually play a moderating role in controlling the disease until he feels the time is right.
The main protagonist Sandra is an oil company PR executive. This choice of profession is important. As a recent Nature review of a book on James Lovelock, of Gaia theory fame, wrote: “If you wanted to be spiritual about it, you could argue that Gaia chose Lovelock as her messenger, despite – or perhaps because of – his evident personal failings. You’d expect a tree-hugger to tell you that the planet is one vast interconnected system powered by life. But when a scientist paid by Shell and Dow Chemical delivers the message, you believe it.” So in my story, it is Anne the environmentalist who dies, and the oil company executive who must stop the disease and save the world (or at least the human part).
The nature of the disease was also carefully chosen, mostly because it is so creepy: a variant of the fungus cordyceps, used later in another apocalyptic drama The Last of Us.
Of course there are many other ways to write a story about the living Earth (see for example David Brin’s Earth). And my screenplay is far from being perfect (it turns out I am better at non-fiction). But if you are a producer thinking to make such a film, or a screenwriter looking for a Gaia-related project, please get in touch – maybe I can save you some trouble this time.

February 23, 2024
The quantum implied volatility model
The quantum implied volatility (QIV) model is a minimalistic model of an implied volatility surface. The aim is to capture the main features of implied volatility using a small number of parameters.
The model is derived by assuming that the implied volatility is the volatility which, when used as input to the Black-Scholes model, will produce the correct option price under the quantum model of asset price. Let x be log price change over a period T, and set z=x/√T. If we ignore the drift term, the quantum model then says that the price distribution can be modelled as a Poisson-weighted sum of Gaussians in z. If we now calculate the volatility which gives the correct option price for that distribution, then we find it satisfies
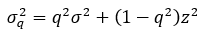
where again z=x/√T but now x represents log moneyness (see here for derivation). The only parameters are a base volatility s, and the number q which has a typical value of about 0.95.
The QIV model was tested against SPX options during the period 2004-2020. The results are shown in the figures below. The left panel shows implied volatility as a function of T and z=x/√T (chosen because the quantum model is expressed in terms of z). The option prices are averaged over each strike and expiration (from five days to one year), and the implied volatility is then computed. Put options are used for x<0 and calls for x≥0. The quantum model is shown by the red line. The right panel is an end view of the same data, which shows that the surface is independent of the period T when plotted in this way.
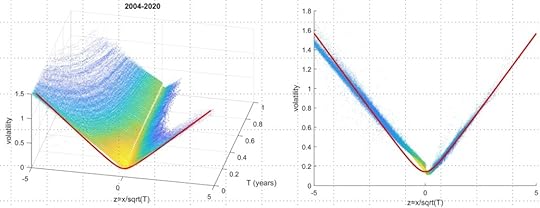
The results are not perfect, especially for at-the-money options, which is not surprising given that implied volatility is complicated by a number of behavioural and other effects. For example, for z near zero, put options (to the left) attract a higher price than call options (to the right). However the quantum model correctly predicts the overall V-shaped configuration that appears when the data is plotted in this way, and does a better job at more extreme strikes. Results could obviously be improved by adding more parameters, but the aim here is to show that the surface can be fit quite well using only the basic model with q=0.95.
For details and other applications of the model, see the paper “A quantum model of implied volatility” in the May 2024 issue of Wilmott. A pre-publication draft is also available here.
February 7, 2024
Quantum economics – real or fake?
Since I started working in quantum economics, a persistent problem was finding suitable venues for publication. Journals in economics or finance wanted nothing to do with it (the exception was Wilmott magazine), so most papers were published in physics journals like Physica A, which meant that no one working in economics ever heard about them. The field clearly needed its own journal! A few years later, with help from many people and Sage Publications, Quantum Economics and Finance was launched.
While my motivation for co-founding the journal was because I wanted the field to succeed, I’ll also admit that there was a selfish interest in that I thought it would give me somewhere to publish my own work – which for some reason often fails to find a home. However it turns out that my papers are so weird, that they are rejected even by my own journal.
The first paper to run into trouble was “A Quantum Oscillator Model of Stock Markets”. One of the main findings is that volatility over a period T is described by the equation
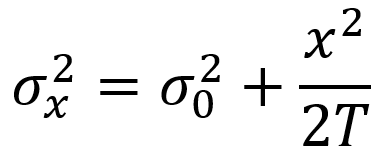
where x is log price change over the same period, adjusted for average drift. The equation was a prediction from the quantum model, and it turned out to hold surprisingly well for a range of asset types including stock market index price data (see figure below for the S&P 500). The formula is useful because it leads to a minimalistic two-parameter model for the implied volatility surface.
 RMS annualized volatility plotted against normalized price change for the S&P 500. The solid lines, from darkest to lightest shades of grey, are for periods of 1, 2, 4 and 8 weeks. Dashed line is the quantum model. Figure from A Quantum Oscillator Model of Stock Markets.
RMS annualized volatility plotted against normalized price change for the S&P 500. The solid lines, from darkest to lightest shades of grey, are for periods of 1, 2, 4 and 8 weeks. Dashed line is the quantum model. Figure from A Quantum Oscillator Model of Stock Markets.What makes the above equation a falsifiable prediction rather than a curve-fitting exercise is that (a) I had no idea it was valid until I tested it and (b) it does not involve any extra parameters, other than a base volatility. Yet when I submitted the paper for review – again, in my own journal! – neither reviewer showed interest in the equation, or its success in modelling empirical price data.
One reviewer in particular wasn’t having it. As they wrote: “the modeling methodology is not appealing. A mass parameter, a fake Plank [sic] constant, and a frequency are introduced to finally describe a quadratic behavior … It is hard to believe that a classical model cannot reproduce the same. Am I right?”
The reviewer here was talking about parameters from different parts of the paper which had no effect on the equation, whose sole parameter is the base volatility. Perhaps they would have found an equation with zero parameters more appealing, less fake?
The paper went to a tie-breaker, who backed publication. Phew!
Next up, “Blinded by Science: The Empirical Case for Quantum Models in Finance”. The theme of this follow-up paper was that people working in economics and finance systematically ignore – or simply do not see – empirical evidence that doesn’t fit their classical assumptions, such as the no-arbitrage principle.
Reviewer 1 nailed the “do not see” thesis right off the bat by stating: “I do not see the point of the paper.” It turned out there was a lot more they didn’t see.
The paper brought out the same equation and pointed out that it was a new finding. The reviewer shot that down by saying that “many models … have considered non-constant volatility.” They were therefore “very confused” by the claim that this was a new result.
On then to Reviewer 2 who wrote that: “This stylized fact is well known … So there is nothing new here … No, nothing leads to this equation which is a purely arbitrary choice of the author, and nothing guarantees that in practice volatility follows [it] (and it is of course not the case).”
So to summarise, the equation is not a prediction, it’s a stylized fact and a purely arbitrary choice which is nothing new and of course not the case and everyone knows it except they don’t because it’s wrong anyway.
The reviewer then swivels their laser-like focus to the somewhat peripheral topic of music theory, because I had remarked as an aside that the energy eigenvalues of the oscillator have frequency ratios of 1, 3, 5 so the tone produced is a major chord. The reviewer set me straight: “it is true that a major chord is composed a the tonic (1), major third (3) and dominant (5), but this has nothing to do with frequencies, only with the position of the notes in the diatonic scale – and actually there are 2 tones between 1 and 3 and 1.5 tone between 3 and 5, therefore the frequency ratios are absolutely not 1, 3 and 5.”
It seemed telling that even for this, a reviewer would rather trust their hazy understanding of theory rather than look at something real, like an actual guitar. A major C chord has notes C, G and E. So if you play these notes, it gives a major C chord:
Note Frequency Ratio to C1
C1 32.703
G2 97.999 2.996636
E3 164.81 5.039599
The other critiques of the paper were no more coherent. One bizarrely insisted that I had mistaken volatility for its square, the variance, perhaps because they “could not see” a square-root sign in front of it.
Apparently there is a new form of therapy called “rejection therapy” where people are counselled to deliberately seek out situations where they are rejected, as a way to build robustness and lose their fear of failure. Quantum economics has certainly proved fruitful as a way to have my work rejected in new and surprising ways, with untold therapeutic benefits.
On a more serious note, though, I think this shows the difficulty in getting new ideas accepted in science, especially if they are in conflict with mainstream results. I have prior form in this area, since I did my D.Phil. on model error in weather forecasting and found it almost impossible to publish papers which pointed out the limitations of weather models. As I wrote in my 2007 book Apollo’s Arrow, a typical pattern was illustrated by one research head who “claimed the research both showed nothing new, and ‘flies in the face of most of the available experimental evidence’.”
I have no idea who the anonymous reviewers for Quantum Economics and Finance were, and because the paper was rejected I didn’t get the chance to respond to them (until now!). But the thing I found strangest about these reviews was that at no point did the reviewers engage with the empirical evidence. It was another example of how experts “do not see” data which contradict longstanding assumptions based on classical theory. They just stated (as one put it) that “there is nothing new here” and “it is of course not the case.” But if the equation for volatility is well-known, provide the references. And if it doesn’t work, show the evidence, instead of dismissing it out of hand.
The paper’s rejection was especially ironic given that it described a number of cases where classical results were widely accepted even when they blatantly contradicted empirical data. Where were the skeptical reviews for those papers?
As I may have mentioned, I am in the fortunate position of having co-founded a journal where I can submit this work, and at least get a hearing. Most researchers, especially people who are new to a field, will of course not have that advantage. Which might explain why the field of economics has been stuck in a time warp for such a long time.
As for critics who call the quantum model “fake”, the country legend Dolly Parton once said “I may look fake but I’m real where it counts.” In fact Parton put this to the test when she entered unannounced a Dolly Parton look-alike contest at a bar – and lost. To a man. Parton herself came last.
Sometimes to tell if a thing is real or fake, looking isn’t enough; you have to listen to the sound it produces.
Which in the case of the quantum model, is a major chord.
November 2, 2023
Interview with E-IR
This interview with E-International Relations was edited by Cécile Pomarède and originally posted here.
Where do you see the most exciting research/debates happening in your field?
In economics, the most exciting project in my view involves building an alternative to mainstream theory that is based on quantum rather than classical thinking. The field of economics has been in a rut for many years. Core ideas like the law of supply and demand date back to the Victorian era, and the failure of models during the financial crisis led to little real change. Newer approaches such as behavioural economics or systems dynamics are certainly useful but have had limited impact, in part because they don’t go far enough. For example, behavioural economics adjusts classical theory without really challenging the central idea of rational utility optimisation.
Quantum economics is a completely new approach because it is based on a different kind of logic. In the classical picture, rational and independent investors drive prices to a stable equilibrium which reflects intrinsic value. In the quantum picture, prices are inherently uncertain, investors are influenced by subjective factors, people are financially and socially entangled, and as a result markets are unstable – and a lot more interesting.
The field is in an exciting stage because quantum models are promising to offer new answers to key problems in economics and finance. For example, one of the oldest such problems is the pricing of options (those financial instruments which give the holder the right to buy or sell an asset at a future date for a set price). The classical theory of option pricing, which is based on the Black-Scholes model from 1973, has been described as the most accurate theory in economics, but the quantum model shows that for commonly-traded options and standard parameters it can be out by 40 percent. The fact that it still serves as the benchmark model is like a magic trick (see also here), where people don’t focus on the obvious flaws because they are distracted by the elegant and persuasive theory.
Advances in the field are also being driven by the development of quantum computing. Mainstream economics was shaped by the development of computers in the post-war era, and quantum computers are changing the way we think about the economy. For example, you can model the financial entanglement between a debtor and creditor as a quantum circuit, and similar circuits are used in quantum cognition to model how we make decisions, or in quantum computers to run artificial intelligence algorithms. Today a high school student can run quantum circuits to model the prisoner’s dilemma game which is new.
How has the way you understand the world changed over time, and what (or who) prompted the most significant shifts in your thinking?
There have been many changes and influences along the way, but to focus on one, my experience doing my D.Phil. on model error in weather forecasting changed the way that I thought about science and made me much more skeptical about things like incentives and the role of mathematical models. At the time there was a belief that weather models could be treated as essentially perfect so all error came from the inputs to the model – i.e. measurement of the current weather – amplified by chaos (the butterfly effect). This meant that forecasters just needed to run many forecasts from perturbed initial conditions, which of course required more computers and bigger budgets. Having worked already on some engineering projects, my view – and that of my supervisor Lenny Smith – was that the main problem wasn’t chaos or the butterfly effect, it was just that models were wrong, because you can’t build a perfect model of the weather. (It’s amusing how people are skeptical about things like quantum approaches, but unskeptical about models once they become established.)
Economics is an example of a field where the dominant ideas only make sense when you think of the incentives involved. During the Cold War, the promotion of results such as the Arrow-Debreu model of competitive equilibrium, which purported to prove the optimality of free markets, was as much about propaganda as science. The efficient market hypothesis – which states that prices adjust to new information immediately – is the economics equivalent of the perfect model hypothesis in weather forecasting because it assumes the equilibrium model is perfect. And mainstream economics, with its emphasis on efficiency, rationality, stability, and optimality, often sounds like the PR wing of the financial sector.
As with many other people (including a significant number of economics students), the 2007/8 crisis, when markets seemed less than stable or efficient, certainly changed the way I thought about economics. The Occupy Wall Street movement in 2011 was kicked off by Adbusters magazine, whose issue at the time featured an extract from my book Economyths, giving a call for economics students to overturn neoclassical orthodoxy and “do something new”. For me, that turned out to be quantum economics.
In recent years, James Der Derian initiated Project Q, Alexander Wendt published Quantum Mind and Social Science, and you are co-editor-in-chief of the new journal Quantum Economics and Finance. Is it fair to say that academia is starting to investigate the implications of quantum discoveries for the social sciences more seriously?
I had the pleasure of meeting Der Derian and Wendt at a quantum conference Wendt organised at Ohio State University in 2018. I really enjoyed the conference because everything seemed so wide open. It’s true that some in academia are starting to take quantum ideas a little more seriously but an interesting question is why it took so long (over a century!), and I would argue there has been a taboo on quantum which is only now being relaxed.
Part of this has to do with some physicists protecting what they see as their turf, but there seems to be a psychological or sociological component as well. One (not universally accepted) theory I put forward in a piece called “A softer economics” is that it relates to the role of gender.
The traditional, billiard-ball view of classical mechanics encodes stereotypically male values like solidity and certainty while quantum, which is based on wave functions and features uncertainty and entanglement, is more yin than yang. Some people get annoyed by the triteness of this idea but for me it seems reasonable, especially given the level of gender bias in both physics and economics. I suspect that if quantum had been discovered by women, instead of a group of young men, we would be calling it the most feminist theory ever. What happened though was that quantum was branded as quantum mechanics, and was considered okay for things like nuclear weapons, but if anyone tried to apply the ideas to human behaviour they were quickly slapped down.
In any case the fact that there has long been a taboo on the use of quantum outside physics, which has only recently been relaxed, is actually a real advantage for a new researcher because when such attitudes change, they tend to change quickly. Certainly, in economics, the number of people involved feels like it is in its exponential growth stage, which is why we decided to start a new journal.
Your new journal Quantum Economics and Finance sheds light on the use of quantum probability as a tool with which to illuminate our understanding of economics and finance. How is this achieved?
To give some background, related fields such as quantum cognition, quantum game theory, and quantum finance have been around for some decades, but there were no specialised journals, so people would end up publishing usually in physics journals where the topic was viewed as a sideshow. I saw the need to start a new journal while researching my book Quantum Economics, and teamed up with Emmanuel Haven who co-authored the book Quantum Social Science and set up the Centre for Quantum Social and Cognitive Science (CQSCS) at Memorial University.. Thanks to the team at Sage Publications we finally managed to get the QEF journal set up earlier this year (2023), with Ray Hawkins joining as managing editor soon after. Emmanuel started his academic career in finance and then went quantum, while Ray trained in quantum physics and then worked in finance, so we have all followed different paths. The editorial board has backgrounds encompassing economics, quantitative finance, mathematics, physics, quantum computing, complexity theory, game theory, psychology, and so on.
Quantum is from the Latin for “how much” and the idea of the journal is that quantum methods apply very well to the economy, where transactions are a way of answering the question “how much?”. The fuzzy notion of value is modelled as a wave function which when measured through transactions collapses down to a number, namely the price. This approach allows us to integrate the dynamical and probabilistic nature of decisions and transactions in a very natural way. In individual decisions, the wave function captures things like subjective factors which don’t appear in the classical analysis. In a model of the stock market, rotations of a quantum wave function represent the level of activity. (As a mental image, think of a skipping rope frozen in the shape of a bell curve. That’s classical probability, of the sort used in traditional theories like Black-Scholes. Now think of the same rope spinning around and distorting with speed, as if someone is actually skipping. That’s the quantum model.)
A basic question of course is whether the quantum approach is justified in an area like economics. The test of this is not whether we think it is permissible to adapt quantum ideas from physics, but a much harder one: it is whether, if the ideas had not existed, economists would have wanted to invent them. So, the aim is to produce models which meet that test, by making useful and accurate predictions.
Of course, what counts in economics is not just the mathematical models, but more broadly the underlying mental model of how things work, and here the quantum framework gives us a richer way of thinking about the economy as being made up of living, uncertain, entangled beings, rather than the classical picture of utility-optimizing “rational economic man”. And the area is very multidisciplinary. It’s interesting to see scientists from quantum computing firms teaming up with psychologists to model cognition, or a sociologist writing about the role of quantum social entanglement in the response to the climate crisis, or a physicist modelling retirement income.
Your proposed quantum approach offers a new insight outside the canon of International Relations to a neglected yet critical topic: the value of money. In what ways has money been overlooked in the study of international affairs?
As I argued in a paper for Security Dialogue, a main insight of the quantum approach is that money has an intrinsically dualistic nature, because it is a way to assign number to value, and these have incompatible properties (for example you can give someone a valuable object, but you can’t give them a number). As with quantum, there is unease around discussing money, and perhaps surprisingly this extends even, or especially, to the field of economics, where money is rarely discussed except as an inert metric, and topics like money creation were long treated as no-go areas, as researchers such as Richard Werner have pointed out.
When I submitted that paper an early reviewer seemed a little befuddled by what they described as a “detour” into the subject of money – even though money is obviously core to how countries interact (US power is related to the US dollar; and if you live in a country with an unstable currency, a dollar or a Euro is not an “inert metric” when you have to pay a debt in it). One thing is that academics working in the social sciences (with exceptions such as the late Susan Strange) may be uninterested in the topic of money, but also have a kind of grudging respect for economists so want to keep off their turf. But most economists have no clue about it either because it doesn’t fit into their classical worldview. In quantum economics, the complex, dualistic nature of money is taken as the starting point.
Could it be argued that information is analogous to money in the global system with the understanding that information is the fabric of the collective consciousness and international entanglement?
Yes, the emphasis on information is important, and it is what makes quantum an appropriate framework for the social sciences. As the quantum computer scientist Scott Aaronson (who is not involved in quantum economics) wrote, quantum probability is “about information and probabilities and observables, and how they relate to each other.” In physics, concepts such as superposition, interference and entanglement are applied to subatomic particles; in the social sciences, they are applied to ideas and information. For example, we can hold two ideas in our head at the same time, and they may interfere, or be entangled with other peoples’ ideas. Money is a particular form of information, which is used to collapse the fuzzy idea of value down to a hard number. There have been many theories of money, but most of these neglect its most basic property, which is its relationship to number.
Are there limitations of applying quantum ontology and methodology to the study of economics, finance, and IR?
Yes, our fascination with ontology is a problem! The interpretation of quantum physics is a topic of endless (if rather specialised) debate in physics. Quantum researchers in social science tend to follow one of two strands, which respond to this debate in different ways.
The first strand is to say that, according to some theories, the brain is based on quantum processes; so if that can be shown to be true, then it will follow that we are quantum and the social sciences need to be quantum too. However, while neurons may indeed turn out to exploit quantum effects, I find this argument to be rather reductionist, and don’t see what difference it would really make to a field such as economics: just because water is quantum doesn’t mean we expect plumbers to retrain in quantum mechanics, because what counts is the emergent properties. Or viewed the other way, the fact that a quantum model works well for something like the stock market doesn’t mean stocks are somehow ontologically at one with electrons.
The second strand, popular in quantum cognition, is the “quantum-like” approach which says we can borrow these models from physics because we are “like” a quantum system. This makes sense if you are trying to explain cognition using physical analogies, or drawing on advanced physics, but if you view quantum as a form of mathematics it doesn’t really work – we don’t say a systems dynamics model is planet-like just because calculus was first applied to planetary motion. And while a mathematical model is related to metaphor, it is different in that for example it can make specific predictions.
Either of these framings lead to confusion about what is “real”. For example, a typical comment (and a reasonable one from a physics perspective) is that a model isn’t “really” quantum because it does not describe “real quantum phenomena.” Yet for someone on a pay-day loan, the entanglement encoded by the information in the debt contract – which again can be written as a quantum circuit – seems pretty real. In general – and this probably comes more naturally to someone trained in the social rather than the physical sciences – information is real, even if it comes from a lawyer rather than the laws of the universe.
While quantum economics does draw on these and other interpretations, it therefore sees quantum probability primarily as a mathematical tool. To quote Aaronson again: “Quantum mechanics is what you would inevitably come up with if you started from probability theory, and then said, let’s try to generalize it so that the numbers we used to call ‘probabilities’ can be negative numbers. As such, the theory could have been invented by mathematicians in the 19th century without any input from experiment. It wasn’t, but it could have been.” It is interesting to think how things would have played out if quantum ideas had been adopted to study human behaviour before they were applied to physics – perhaps physicists would be worrying over whether it was intellectually defensible to model electrons as being like little people.
Again, the test of the quantum approach isn’t whether we have somehow inherited quantum properties such as superposition and entanglement from subatomic particles. Instead, the idea is more in the spirit of the first quantum pioneers, which is to take quantum social properties at face value, and use mathematics in a creative way to model observed phenomena. Viewed this way, attempts to relate everything to physics or create a unified ontology are something of a distraction. And we certainly have urgent problems where a quantum perspective would be useful. An example is the climate crisis, which could be viewed as the logical consequence of classical economics, the end result of individual utility-maximizing behaviour. One focus of the QEF journal is to investigate how quantum ideas can help loosen our doomed obsession with a particular type of economic growth.
In Economyths: 10 ways economics gets it wrong; you highlight the intellectual poverty of neo-classical economics. What are the ways in which economics gets it wrong?
The ten chapters in the original 2010 book were about ideas such as rationality, stability, individuality, and so on which characterise the classical picture of the economy (as opposed to the actual economy). The inspiration for this traditional view is often considered to be Newtonian science, but the ideas actually go back a lot further – in fact the chapter topics were based on a list of ten opposites from the Pythagoreans in ancient Greece. In a revised edition from 2017 I added an extra topic which combined aspects of the others, namely the (again, counterintuitive) fact that economics ignores or downplays the topic of money. This has left economists singularly unequipped to understand how much of the economy actually works. In Canada, for example, the economy is dominated by a housing bubble which economists try to analyse based on the mechanics of supply and demand, but is better understood from a quantum perspective as a money creation scheme – the financial version of a nuclear device – where the banks and some property owners are enriched, but the society as a whole is destabilised.
As Wendt noted in 2005 the same classical ideas have permeated the social sciences, and are backed up in part because of the (now somewhat tarnished) prestige of economics, which is associated with “hard” mathematics. So a first step for quantum economics is to build empirically-grounded alternatives to things like the “law of supply and demand”, the pricing of risk, and so on which out-perform the classical approach. Of course, not all models need to be quantum (and there is no such thing as a perfect model!), but together with other heterodox approaches like systems dynamics, complexity, ecological economics and so on the quantum approach can help reinvent economics. You don’t need to be a quantum expert to get involved.
How do you find inspiration to think innovatively and come up with unorthodox ideas, at the intersection of different academic disciplines?
One thing is that I trained in mathematics which allowed me to work across disciplines, including engineering, forecasting, systems biology, and economics (it probably helped that my jobs kept ending; for example, I returned to university after a particle accelerator project I was working on, the Superconducting Super Collider, was cancelled). However, another thing is the combination of science with writing for a general audience, which has been a great way to see topics from different angles. I credit this interest in part to familial influence – my father was an English professor – and also to my undergraduate university (Alberta) where mathematics could be taken as an arts subject, so I got to combine it with things like philosophy, art history, Shakespeare, film studies, and so on (even quantum physics). I also draw inspiration from my wife who as an architect works at the interface of art and engineering.
What would you say is the most important advice for a young scholar in IR?
I don’t really feel qualified to answer this one, but (since I’m here) I think the most important advice would be to NOT go into quantum. Sure, the methods can work. Yes, there are low-hanging fruit for early adopters. Okay, it is new and fun. And it is certainly true that the classical approach has failed, or at least run out of tarmac. But any rational person knows that it would be much better to keep in a safe, respected area rather than go down some weird and risky quantum path where the end point, if there is one, is highly uncertain. Of course, a few people will ignore this sensible advice, and we look forward to hearing about their work and maybe receiving their submissions at the journal.
See here for the original interview at E-IR.
June 15, 2023
CQF talk on a quantum view of Black-Scholes
It was a pleasure speaking yesterday at the Quant Insights conference marking the 50th anniversary of the Black-Scholes model. My talk presented nine predictions which came out of the quantum model – things that I had not been aware of, but that were suggested by the model and proved correct after empirical tests. And they all had implications for option pricing and the Black-Scholes model.

1. Before starting to work with the model, I didn’t know that price change and volatility for index data such as the S&P 500 or DJIA scale inversely with the square-root of time, even though the price change data is not normal, and volatility is not constant.
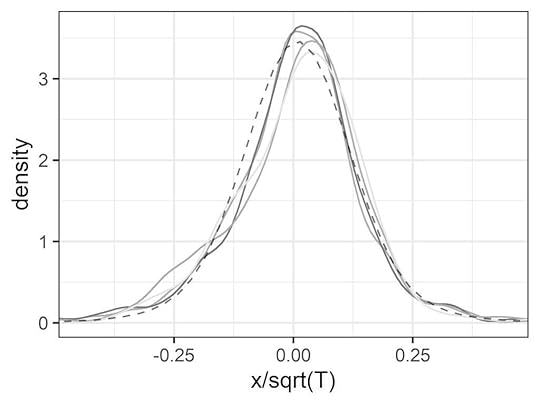 Density plots of log price changes, normalized by the square-root of time in years, for the S&P 500 over the years 1992-2021. The solid lines, from darkest to lightest shades of grey, are for periods of 1, 2, 4 and 8 weeks (measured in days). Dashed line is the quantum model.
Density plots of log price changes, normalized by the square-root of time in years, for the S&P 500 over the years 1992-2021. The solid lines, from darkest to lightest shades of grey, are for periods of 1, 2, 4 and 8 weeks (measured in days). Dashed line is the quantum model.2. I had heard of the square-root law of price impact, which says that the price change induced by a large order scales with the square-root of the order size, but didn’t know that the numerical coefficient was approximately one, as predicted by the quantum model.
 Plot of price change versus order size Q over average daily volume V follows a square-root law with coefficient near unity.
Plot of price change versus order size Q over average daily volume V follows a square-root law with coefficient near unity.3. I certainly didn’t know that the variance followed a simple equation that contradicted a published result.
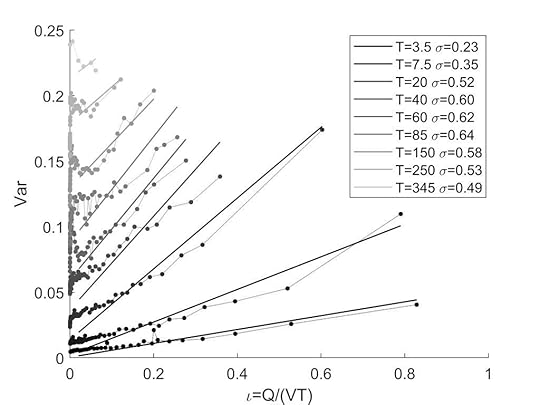 Variance plotted against imbalance Q/(VT) where Q is order size, V is daily volume, and order time T ranges from 3.5 minutes (black) to 345 minutes (light grey). The single parameter sigma estimates the volatility.
Variance plotted against imbalance Q/(VT) where Q is order size, V is daily volume, and order time T ranges from 3.5 minutes (black) to 345 minutes (light grey). The single parameter sigma estimates the volatility.The drawbacks of the neoclassical model of supply and demand have long been pointed out by critics such as Steve Keen. A basic one is that what counts is not supply and demand separately, but the ratio of demand to supply for available units. The quantum price impact model therefore gives an alternative model with only a single parameter, that has been rigorously tested for stock market data.
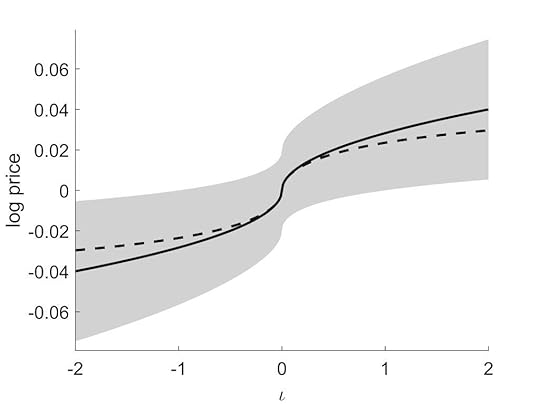 Plot of log price against imbalance, which is the ratio of demand to supply per available unit.
Plot of log price against imbalance, which is the ratio of demand to supply per available unit.4. I had heard of the implied volatility smile in options trading, but didn’t know that actual volatility showed an even more pronounced smile, that followed a simple relationship with price change and time (and is related to price impact). Nor had I seen this fact, or the connection with implied volatility, reported in the literature.
 RMS annualized volatility for the S&P 500, plotted against normalized price change, for periods of 1, 2, 4 and 8 weeks (dark to light). Dashed line is the quantum prediction.
RMS annualized volatility for the S&P 500, plotted against normalized price change, for periods of 1, 2, 4 and 8 weeks (dark to light). Dashed line is the quantum prediction.5. Implied volatility is not the same as actual volatility, because it is found by fitting a lognormal option pricing model to data that is not actually lognormal, and is affected by trader behaviour. So it was interesting to find that the quantum model produced an implied volatility surface very similar to what is found in the wild.
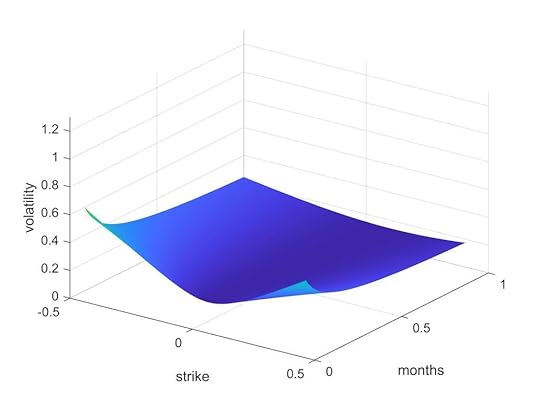 The quantum implied volatility surface is a somewhat flattened version of actual volatility.
The quantum implied volatility surface is a somewhat flattened version of actual volatility.6. The VIX index is an estimate of future volatility based on implied volatility, which is in turn used to price other options. The VIX is often described as being model independent, but its formula is based on two things: that volatility is independent of strike, and that the relevant growth rate is the risk-free rate. The former is an assumption of the Black-Scholes model, while the latter is its key finding. The VIX is therefore Black-Scholes in another guise. The quantum model predicted that the VIX substantially over-estimates both implied volatility and actual volatility, because its formula adds up the contributions of options in the wrong way. The results agree.
 The VIX is produced using a formula which assigns weights to options (grey line) and produces a single volatility (dashed line) which is supposed to represent the implied volatilities (blue points). The quantum model (red) is a version of the smile curve.
The VIX is produced using a formula which assigns weights to options (grey line) and produces a single volatility (dashed line) which is supposed to represent the implied volatilities (blue points). The quantum model (red) is a version of the smile curve.7. Given that the Black-Scholes model assumes constant volatility, it makes sense that it should misprice options. However I for one was surprised to find that, according to the quantum model, it misprices at-the-money straddle options by a factor about equal to the square-root of two.
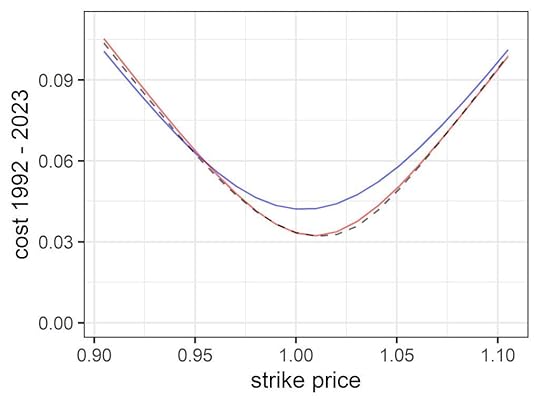 Comparison of straddle option pay-in for Black-Scholes model (blue) and quantum model (red), with expected pay-out (dashed). The Black-Scholes model misprices at-the-money straddles by about 40 percent.
Comparison of straddle option pay-in for Black-Scholes model (blue) and quantum model (red), with expected pay-out (dashed). The Black-Scholes model misprices at-the-money straddles by about 40 percent.8. Since the Black-Scholes model is the industry-standard pricing model, it makes sense that model error will lead to mispricing in option markets. This prediction was verified by Larry Richards who analyzed CBOE data for over 25,000 1-month SPX option prices from 2004 to 2017. So much for efficient markets. See our paper published in the March 2023 issue of Wilmott.
9. Finally, a logical consequence of this is that one can devise options-trading strategies to exploit this mispricing – for example, by selling at-the-money straddles (with appropriate protection to cover potential losses).
To summarise, the main difference between the classical random walk model traditionally used in quantitative finance, and the quantum model, is that the former assumes markets are at equilibrium and volatility is constant, while the latter treats markets as a dynamical system where price change and volatility are linked. The quantum model therefore does a better match of fitting and predicting market behaviour, without relying on additional made-up parameters of the sort so common in traditional quant finance.
In a panel discussion in which quants Emanuel Derman and Robert Litterman reminisced about the history of the Black-Scholes model, a viewer asked Derman whether “quantum economics and finance was too much of a stretch.” He agreed (again, predictably) that yes it was, without giving specific reasons. And yet it’s strange that previous studies of implied volatility – including Derman’s own book The Volatility Smile – didn’t pick up on the obvious fact that the implied volatility smile is a weaker version of a smile seen in the actual asset price data (see my article The Black-Scholes Magic Trick in the July 2023 issue of Wilmott). Or that this would lead to a significant mispricing of commonly-traded options.
Models aren’t just tools to analyze systems, they also affect what we do and don’t see. And in finance, the quantum model isn’t too much of a stretch – it’s a perfect fit. For details of the quantum model, see here. And for more work along these lines, please follow our new journal Quantum Economics and Finance.



