Smooth numbers and max-entropy
Given a threshold 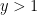 , a
, a  -smooth number (or
-smooth number (or  -friable number) is a natural number
-friable number) is a natural number  whose prime factors are all at most
whose prime factors are all at most  . We use
. We use 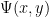 to denote the number of
to denote the number of  -smooth numbers up to
-smooth numbers up to  . In studying the asymptotic behavior of
. In studying the asymptotic behavior of 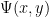 , it is customary to write
, it is customary to write  as
as 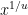 (or
(or  as
as 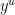 ) for some
) for some 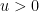 . For small values of
. For small values of  , the behavior is straightforward: for instance if
, the behavior is straightforward: for instance if 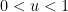 , then all numbers up to
, then all numbers up to  are automatically
are automatically  -smooth, so
-smooth, so
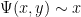
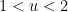 , the only numbers up to
, the only numbers up to  that are not
that are not  -smooth are the multiples of primes
-smooth are the multiples of primes 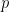 between
between  and
and  , so
, so
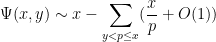
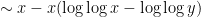

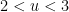 , there is an additional correction coming from multiples of two primes between
, there is an additional correction coming from multiples of two primes between  and
and  ; a straightforward inclusion-exclusion argument (which we omit here) eventually gives
; a straightforward inclusion-exclusion argument (which we omit here) eventually gives
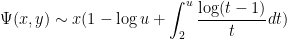
More generally, for any fixed 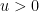 , de Bruijn showed that
, de Bruijn showed that
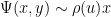
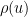 is the Dickman function. This function is a piecewise smooth, decreasing function of
is the Dickman function. This function is a piecewise smooth, decreasing function of  , defined by the delay differential equation
, defined by the delay differential equation
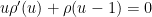
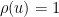 for
for 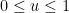 .
. The asymptotic behavior of 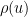 as
as 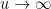 is rather complicated. Very roughly speaking, it has inverse factorial behavior; there is a general upper bound
is rather complicated. Very roughly speaking, it has inverse factorial behavior; there is a general upper bound 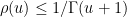 , and a crude asymptotic
, and a crude asymptotic
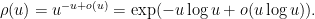
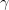 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 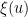 is defined implicitly by the equation One cannot write
is defined implicitly by the equation One cannot write 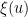 in closed form using elementary functions, but one can express it in terms of the Lambert
in closed form using elementary functions, but one can express it in terms of the Lambert 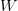 function as
function as 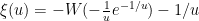 . This is not a particularly enlightening expression, though. A more productive approach is to work with approximations. It is not hard to get the initial approximation
. This is not a particularly enlightening expression, though. A more productive approach is to work with approximations. It is not hard to get the initial approximation 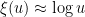 for large
for large  , which can then be re-inserted back into (3) to obtain the more accurate approximation
, which can then be re-inserted back into (3) to obtain the more accurate approximation
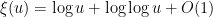
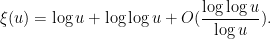
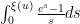 to
to
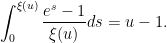
This asymptotic (2) is quite complicated, and so one does not expect there to be any simple argument that could recover it without extensive computation. However, it turns out that one can use a “maximum entropy” to get a reasonably good heuristic approximation to (2), that at least reveals the role of the mysterious function 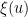 . The purpose of this blog post is to give this heuristic.
. The purpose of this blog post is to give this heuristic.
Viewing 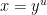 , the task is to try to count the number of
, the task is to try to count the number of  -smooth numbers of magnitude
-smooth numbers of magnitude 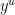 . We will propose a probabilistic model to generate
. We will propose a probabilistic model to generate  -smooth numbers as follows: for each prime
-smooth numbers as follows: for each prime 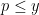 , select the prime
, select the prime 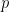 with an independent probability
with an independent probability 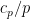 for some coefficient
for some coefficient 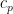 , and then multiply all the selected primes together. This will clearly generate a random
, and then multiply all the selected primes together. This will clearly generate a random  -smooth number
-smooth number  , and by the law of large numbers, the (log-)magnitude of this number should be approximately (where we will be vague about what “
, and by the law of large numbers, the (log-)magnitude of this number should be approximately (where we will be vague about what “ ” means here), so to obtain a number of magnitude about
” means here), so to obtain a number of magnitude about 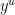 , we should impose the constraint
, we should impose the constraint
The indicator 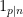 of the event that
of the event that 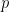 divides this number is a Bernoulli random variable with mean
divides this number is a Bernoulli random variable with mean 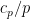 , so the Shannon entropy of this random variable is
, so the Shannon entropy of this random variable is
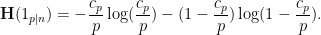
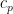 is not too large, then Taylor expansion gives the approximation
is not too large, then Taylor expansion gives the approximation
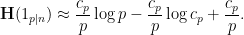
 is
is
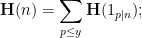
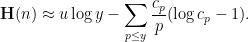
 that are typically generated by this random process should be approximately
that are typically generated by this random process should be approximately
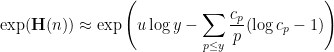
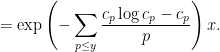
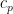 are chosen to maximize the right-hand side subject to the constraint (5).
are chosen to maximize the right-hand side subject to the constraint (5).One could solve this constrained optimization problem directly using Lagrange multipliers, but we simplify things a bit by passing to a continuous limit. We take a continuous ansatz 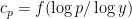 , where
, where ![{f: [0,1] \rightarrow {\bf R}}](https://i.gr-assets.com/images/S/compressed.photo.goodreads.com/hostedimages/1758024784i/37228729.png) is a smooth function. Using Mertens’ theorem, the constraint (5) then heuristically becomes and the expression (6) simplifies to So the entropy maximization problem has now been reduced to the problem of minimizing the functional
is a smooth function. Using Mertens’ theorem, the constraint (5) then heuristically becomes and the expression (6) simplifies to So the entropy maximization problem has now been reduced to the problem of minimizing the functional 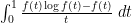 subject to the constraint (7). The astute reader may notice that the integral in (8) might diverge at
subject to the constraint (7). The astute reader may notice that the integral in (8) might diverge at 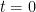 , but we shall ignore this technicality for the sake of the heuristic arguments.
, but we shall ignore this technicality for the sake of the heuristic arguments.
This is a standard calculus of variations problem. The Euler-Lagrange equation for this problem can be easily worked out to be
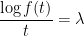
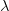 ; in other words, the optimal
; in other words, the optimal 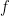 should have an exponential form
should have an exponential form 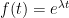 . The constraint (7) then becomes
. The constraint (7) then becomes
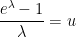
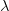 is precisely the mysterious quantity
is precisely the mysterious quantity 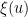 appearing in (2)! The formula (8) can now be evaluated as
appearing in (2)! The formula (8) can now be evaluated as
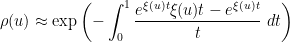
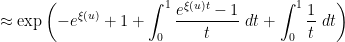
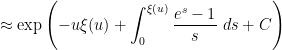
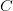 is the divergent constant
is the divergent constant
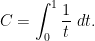
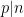 is unrealistic when trying to confine
is unrealistic when trying to confine  to a single scale
to a single scale  ; this comes down ultimately to the subtle differences between the Poisson and Poisson-Dirichlet processes, as discussed in this previous blog post, and is also responsible for the otherwise mysterious
; this comes down ultimately to the subtle differences between the Poisson and Poisson-Dirichlet processes, as discussed in this previous blog post, and is also responsible for the otherwise mysterious 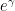 factor in Mertens’ third theorem; it also morally explains the presence of the same
factor in Mertens’ third theorem; it also morally explains the presence of the same 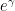 factor in (2). A related issue is that the law of large numbers (4) is not exact, but admits gaussian fluctuations as per the central limit theorem; morally, this is the main cause of the
factor in (2). A related issue is that the law of large numbers (4) is not exact, but admits gaussian fluctuations as per the central limit theorem; morally, this is the main cause of the 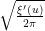 prefactor in (2).
prefactor in (2).Nevertheless, this demonstrates that the maximum entropy method can achieve a reasonably good heuristic understanding of smooth numbers. In fact we also gain some insight into the “anatomy of integers” of such numbers: the above analysis suggests that a typical  -smooth number
-smooth number  will be divisible by a given prime
will be divisible by a given prime 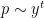 with probability about
with probability about 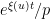 . Thus, for
. Thus, for 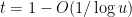 , the probability of being divisible by
, the probability of being divisible by 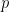 is elevated by a factor of about
is elevated by a factor of about 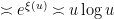 over the baseline probability
over the baseline probability 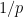 of an arbitrary (non-smooth) number being divisible by
of an arbitrary (non-smooth) number being divisible by 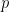 ; so (by Mertens’ theorem) a typical
; so (by Mertens’ theorem) a typical  -smooth number is actually largely comprised of something like
-smooth number is actually largely comprised of something like 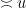 prime factors all of size about
prime factors all of size about 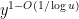 , with the smaller primes contributing a lower order factor. This is in marked contrast with the anatomy of a typical (non-smooth) number
, with the smaller primes contributing a lower order factor. This is in marked contrast with the anatomy of a typical (non-smooth) number  , which typically has
, which typically has 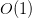 prime factors in each hyperdyadic scale
prime factors in each hyperdyadic scale ![{[\exp\exp(k), \exp\exp(k+1)]}](https://i.gr-assets.com/images/S/compressed.photo.goodreads.com/hostedimages/1758024785i/37228748.png) in
in ![{[1,n]}](https://i.gr-assets.com/images/S/compressed.photo.goodreads.com/hostedimages/1758024785i/37228749.png) , as per Mertens’ theorem.
, as per Mertens’ theorem.
Terence Tao's Blog
- Terence Tao's profile
- 230 followers



