I’ve always liked to play with mathematics, and I’ve always been curious about this strange world of higher dimensions and infinities that somehow add up to -1/12. Geometry was one of the most enjoyable classes I took in high school, and although it took me a while to get accustomed to it, algebra and trigonometry also became engrossing. I never progressed very far into the world of math, but I’ve always been curious and find myself, in odd times, playing with numbers in my head.

One of the things I like to do is play with prime numbers. I like the feel of them, their atomic solidity. I like how they work together to build larger, composite numbers. And I like taking a random number and trying to figure out its factors. That’s not exactly high mathematics, but it’s fun. Take 115, for example. That breaks down into 5 and 23. 105 breaks into a 3, 5, and 7. 110 is made up of 2, 5, and 11. So even though the numbers are only 10 apart, you manage to catch all the starting primes: 2, 3, 5, 7, 11, and then a larger, stranger creature, 23. 6 new primes in just 10 spaces! I like the idea of numbers being constructions, being made of other numbers. The patterns in it, the hidden structure inside apparent solidity. Who would have thought that 117 is not prime? It’s actually built of 3, 3, and 13. I like that kind of thing. There’s a poetry to it and a satisfying wholeness to the constructive quality of mathematics.

This interest in primes is not new. I’ve been kicking them around for quite a while. A decade or so ago, I was writing a novel about the birth of computers called “So Much Better Than Life”. I never finished it (or I haven’t finished yet), but I found this passage:

William White did have one talent, even if he cared little for it. He was very good at numbers. There was a certain mechanical surety to arithmetic that appealed to him. His mother, Gwendolyn White, a slim, pale beauty, had once brought him home from the Boston Public Library a book concerning numbers, and he read it several times. Since then, at night, when the world seemed a vast, purposeless void, and his bones shivered in disgust, William would break down numbers into their primes. It lulled him to sleep. He would see the numbers in his head, watch them break up into their constituent primes and float downwards in his mind’s perception until those lovely, unfissionable primes would come to settle upon the bed of his mind like feathery snow. Twenty-five wafted down into two beautifully symmetrical fives. Sixty-eight tumbled into an admirable pair of stalwart twos and a stern seventeen, a number he always associated with the color blue and his father. One hundred and twenty three, such a pedantic number, obligingly broke into a flirtatious three and the mysterious, possibly conspiratorial number forty-one. And so on into the darkness of the night until, buried in a drift of primes, he fell peacefully asleep. 

This snowfall of primes apparently stuck with me. When it came time to decide what to do for my second game for iOS, I decided to start with this fall of prime numbers. I felt I had learned enough from my first game to tackle something more complicated, and something I didn’t know much about. To paraphrase Gauss, if I am not learning while I’m doing something, I probably won’t do it. I wanted a chance to dive into primes, and it turned out to be a world much, much more complex and interesting than I understood. Primes are integrated into the very soul of mathematics, and developing this wonderful game became a vast exploration of the history of mathematics and mathematical ideas.

Prime Flow began as that snowfall of primes. This quickly developed into the idea of maintaining a flow by picking out primes from a rain of random numbers. Patterns emerge and vanish, and larger primes appear as the field increases in speed. For me, it was a way of exploring higher numbers easier, and to explore prime numbers in a way that was fun and easy.

To my surprise, what I thought would be a very complicated build, developed fairly easily, as if the game wanted to be built. I added layers of mathematical history as achievement unlocks and math animations to explain some of the famous prime series, like the Sophie Germain primes which are found at 2p +1, with p being prime and the result also being prime. For example, 2 and 5 are Sophie Germain primes and also 5 and 11. Sophie Germain was a mathematician who had to publish under a male name, and is just one of the parade of mathematicians who march through Prime Flow, a vast and diverse group of characters whose exploits are comparable to poets: dueling, pseudonyms, madness, world travel, etcetera.

Sophie Germain, one of the fascinating characters I met during work on Prime Flow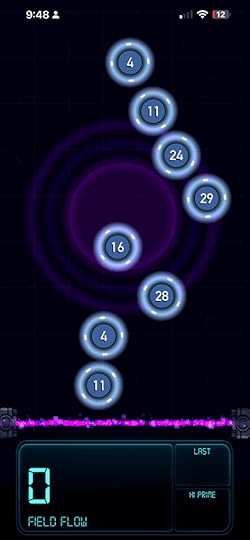

In the game, numbers float down the screen. If you pick up a prime, the Field Flow increases, and the random numbers become larger. But the field moves faster. If you hit a composite number, the amount is subtracted from the Field Flow and the number falls away. Also, if a prime number hits the laser at the bottom, its number will be subtracted from the Field Flow. When the Field Flow drops below zero, the run ends. The object of the game is to get the highest score which is calculated by the highest prime you were able to collect, the number of patterns you found in the primes (for example, collecting a 2 and 5 rewards you a Sophie Germain pattern), and the amount of primes you collected in total.

For me the great joy of this game was the fascinating history of mathematics from Pythagoras to Terence Tao. I learned every day making this game, and it was exhilarating. But perhaps the thing I am proud of the most is that the game seems like an exploration, like the kind of dreaming that my character was doing in my as-yet-unfinished novel: a dream of numbers being sifted to their essence. For me, the game has been very much like the poetry I write. I don’t know who cares or who asked for such a thing, but I do what I do because it moves me, it interests me. I find it engaging. If others do too, that’s great. If not, meh.

The game will have no ads or in-game purchases. I might add on to it when the mood strikes me. It’s a lovely piece of mathematical exploration, so if you like numbers, you’ll enjoy hanging out with the game in your odd time. If you really want to dig deeper into math, the game will point you in interesting directions, but if you just want a high score, it will accommodate you. It’s the kind of game I wish I had in high school when I first loved geometry. It’s a game about the sheer beauty and fascination of numbers.

I hope everyone enjoys it and finds it as engaging as I do!

Otherwise, why bother?

You can begin exploring prime numbers with Prime Flow here:

https://apps.apple.com/us/app/prime-flow/id6757245218

Share this with someone who likes math. I’m really interested in what people think!