As seen in QEF15, stock market data follows q-variance and the q-distribution. Q-variance refers to the property that the expected variance of log returns x, corrected for drift, over a period T follows to good approximation the formula V(z)=σ^2+z^2/2 where z=x∕√T. This property follows because we model price change as the displacement of a quantum harmonic oscillator, so a larger displacement is associated with higher energy and therefore higher volatility.

The probability distribution associated with q-variance is a Poisson-weighted sum of Gaussians known as the q-distribution. The Poisson rate parameter is λ=0.5 and the standard deviation for each term is σ_n=σ√(1+2n).

The q-distribution can be used to calculate the price of a call option. We can also use it to calculate the q-implied volatility σ_q, which is the volatility to be used in the Black-Scholes model for this distribution. The answer is seen to be

σ_q^2=q^2 σ^2+(1-q^2 ) z^2   

where q≅0.95.

We can therefore compare three kinds of volatility. Q-implied volatility is the number suggested by quantum model. Implied volatility is the number used by traders. Payout-implied volatility is the number which corresponds to average payouts.

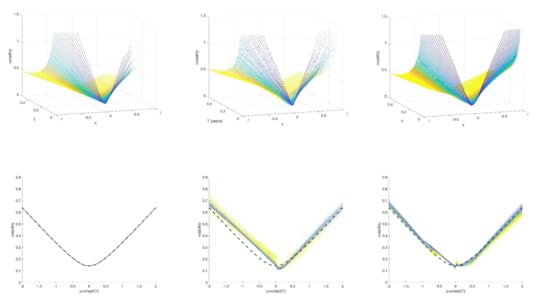Plots show q-implied (left), implied (middle), and payout-implied (right) volatility
as a function of x and T (top row) and z only (bottom row).

To summarise, the q-distribution can be used to calculate the expected payout of a call option. The q-implied volatility (the volatility suggested by the quantum model) is quite close to both implied volatility (the volatility used by traders) and payout-implied volatility (the volatility which reflects average payout)

This suggests that markets follow a quantum distribution, and traders are using a quantum model to price options – they just don’t know it

For further reading, see:

Orrell D (2025) A Quantum of Variance, and the Challenge for Finance. Wilmott 2025(138).

Orrell D (2025) A Quantum Jump Model of Option Pricing. Journal of Derivatives 33(1).

Previous: QEF15 – A quantum oscillator model of stock markets 2: q-variance and the q-distribution

Playlist: Quantum Economics and Finance